正余弦三角函数公式大全：正弦与余弦三角函数公式大全，完全解析与学习宝典

三角函数是数学中重要的基础内容，尤其在几何、物理和工程学中有着广泛的应用，正弦（sin）和余弦（cos）作为最基本的三角函数，其公式体系复杂而精妙，本文将系统梳理正弦与余弦函数的常用公式，包括定义、诱导公式、和差角公式、倍角公式、半角公式等,帮助读者全面掌握三角函数的核心知识。

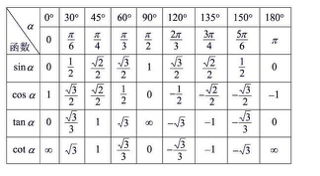
正弦与余弦函数的定义

在单位圆中，设角θ的终边与单位圆交于点P(x, y),则：

• 余弦函数：cosθ = x
• 正弦函数：sinθ = y

在直角三角形中，设角θ的对边为a，邻边为b，斜边为c,则：

• sinθ = a/c
• cosθ = b/c

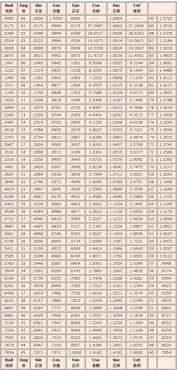
诱导公式

诱导公式用于将任意角的三角函数值转化为锐角三角函数值，便于计算和记忆,以下是常见的诱导公式：

1. sin(π + θ) = -sinθ
2. sin(π - θ) = sinθ
3. sin(-θ) = -sinθ
4. cos(π + θ) = -cosθ
5. cos(π - θ) = -cosθ
6. cos(-θ) = cosθ
7. sin(2π + θ) = sinθ
8. cos(2π + θ) = cosθ

记忆口诀：奇变偶不变，符号看象限。

• “奇变”指角度为π/2的奇数倍时，函数名称变为余函数（sin变cos，cos变sin）；
• “偶不变”指角度为π/2的偶数倍时，函数名称不变；
• “符号看象限”指将角度化为锐角后,根据原角所在象限确定符号。

和差角公式

和差角公式用于计算两个角的和或差的三角函数值：

1. sin(α + β) = sinα cosβ + cosα sinβ
2. sin(α - β) = sinα cosβ - cosα sinβ
3. cos(α + β) = cosα cosβ - sinα sinβ
4. cos(α - β) = cosα cosβ + sinα sinβ

这些公式是推导其他三角函数公式的基础,也是解决复杂三角问题的关键。

倍角公式

倍角公式用于计算二倍角的三角函数值：

1. sin(2θ) = 2 sinθ cosθ
2. cos(2θ) = cos²θ - sin²θ = 2cos²θ - 1 = 1 - 2sin²θ

倍角公式可以进一步推导出三倍角、四倍角等更高阶的公式,但掌握二倍角公式是基础。

半角公式

半角公式用于计算半角的三角函数值：

1. sin(θ/2) = ±√((1 - cosθ)/2)
2. cos(θ/2) = ±√((1 + cosθ)/2)
3. tan(θ/2) = ±√((1 - cosθ)/(1 + cosθ))

半角公式在积分、微分方程和物理中常被使用，符号的选择取决于θ所在象限。

万能公式

万能公式将三角函数转化为正切函数的一半角形式：

1. sinθ = 2 tan(θ/2) / (1 + tan²(θ/2))
2. cosθ = (1 - tan²(θ/2)) / (1 + tan²(θ/2))
3. tanθ = 2 tan(θ/2) / (1 - tan²(θ/2))

万能公式在积分和微分方程中尤为有用。

其他常用公式

1. sin²θ + cos²θ = 1（毕达哥拉斯恒等式）
2. 1 + tan²θ = sec²θ
3. 1 + cot²θ = csc²θ

这些恒等式是三角函数运算的基础,常用于化简和证明。

应用提示

• 记忆技巧：通过口诀、图表和反复练习来加深记忆。
• 解题思路：根据问题类型选择合适的公式，如和差角公式用于求和，倍角公式用于化简。
• 常见错误：注意角度单位（弧度制或角度制）、符号选择、恒等式的正确应用。

正弦与余弦三角函数公式是数学学习中的核心内容，掌握这些公式不仅能帮助解决数学问题，还能为后续学习高等数学、物理和工程打下坚实基础，希望本文能为读者提供清晰、全面的公式梳理，助您在学习中游刃有余,轻松应对各类三角函数问题。

如需PDF格式或PPT演示版,可联系获取。