初中三角函数的公式大全:初中三角函数公式大全,掌握这些公式轻松解题!
三角函数的基本概念
三角函数是描述角度与边长关系的函数,主要包括正弦(sin)、余弦(cos)、正切(tan)、余切(cot)、正割(sec)和余割(csc),在初中阶段,主要涉及的是正弦、余弦和正切。
- 正弦(sin):对边长度除以斜边长度。
- 余弦(cos):邻边长度除以斜边长度。
- 正切(tan):对边长度除以邻边长度。
三角函数的基本关系式
平方关系: [ \sin^2\theta + \cos^2\theta = 1 ] [ 1 + \tan^2\theta = \sec^2\theta ] [ 1 + \cot^2\theta = \csc^2\theta ]
倒数关系: [ \sin\theta \cdot \csc\theta = 1 ] [ \cos\theta \cdot \sec\theta = 1 ] [ \tan\theta \cdot \cot\theta = 1 ]

特殊角的三角函数值
掌握特殊角的三角函数值是解题的关键,以下是常见的特殊角:
| 角度(度) | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sinθ | 0 | 1/2 | √2/2 | √3/2 | 1 |
| cosθ | 1 | √3/2 | √2/2 | 1/2 | 0 |
| tanθ | 0 | √3/3 | 1 | √3 | 无定义 |
诱导公式
诱导公式用于将任意角的三角函数转化为锐角三角函数,常见的有:
角与π±α的关系: [ \sin(\pi + \alpha) = -\sin\alpha ] [ \cos(\pi + \alpha) = -\cos\alpha ] [ \tan(\pi + \alpha) = \tan\alpha ]
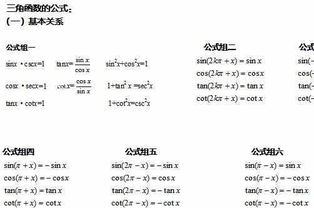
角与2π±α的关系: [ \sin(2\pi + \alpha) = \sin\alpha ] [ \cos(2\pi + \alpha) = \cos\alpha ] [ \tan(2\pi + \alpha) = \tan\alpha ]
和角公式与差角公式
和角公式: [ \sin(\alpha + \beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta ] [ \cos(\alpha + \beta) = \cos\alpha\cos\beta - \sin\alpha\sin\beta ] [ \tan(\alpha + \beta) = \frac{\tan\alpha + \tan\beta}{1 - \tan\alpha\tan\beta} ]
差角公式: [ \sin(\alpha - \beta) = \sin\alpha\cos\beta - \cos\alpha\sin\beta ] [ \cos(\alpha - \beta) = \cos\alpha\cos\beta + \sin\alpha\sin\beta ] [ \tan(\alpha - \beta) = \frac{\tan\alpha - \tan\beta}{1 + \tan\alpha\tan\beta} ]

二倍角公式
二倍角公式是和角公式的特例,常用于简化计算:
正弦二倍角公式: [ \sin(2\theta) = 2\sin\theta\cos\theta ]
余弦二倍角公式: [ \cos(2\theta) = \cos^2\theta - \sin^2\theta = 2\cos^2\theta - 1 = 1 - 2\sin^2\theta ]
正切二倍角公式: [ \tan(2\theta) = \frac{2\tan\theta}{1 - \tan^2\theta} ]
记忆技巧与学习建议
- 理解优先于记忆:三角函数公式较多,理解其推导过程比死记硬背更有效。
- 多做练习题:通过大量练习,熟悉公式的应用场景。
- 利用单位圆:单位圆可以帮助你直观理解三角函数的定义和变化规律。
- 归纳总结:将公式分类整理,形成知识网络,便于复习和记忆。
三角函数是初中数学的重要组成部分,掌握其公式和应用方法,不仅能提高解题能力,还能为高中阶段的数学学习打下坚实基础,希望本文的公式大全能帮助你轻松应对三角函数的学习和考试!
文章已关闭评论!