三角函数对照表角度表0到90:三角函数角度表0到90度,数学学习必备参考
三角函数是数学中一个非常重要的概念,广泛应用于几何、物理、工程等领域,在学习三角函数时,掌握不同角度下的函数值是基础中的基础,本文将详细介绍0°到90°范围内常见角度的三角函数值,帮助你快速记忆和应用。
三角函数的基本概念
三角函数主要包括正弦(sin)、余弦(cos)和正切(tan)三个基本函数,对于任意角θ,其定义如下:
- 正弦(sinθ):对边长度与斜边长度的比值。
- 余弦(cosθ):邻边长度与斜边长度的比值。
- 正切(tanθ):对边长度与邻边长度的比值。
在直角三角形中,θ是其中一个锐角(0° < θ < 90°),则上述定义成立。
0°到90°角度的三角函数值表
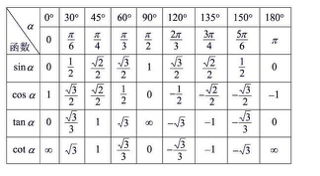
以下是0°到90°之间常见角度的三角函数值表,包含sin、cos、tan三个函数的值:
| 角度(°) | sinθ | cosθ | tanθ |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 30 | 1/2 | √3/2 | √3/3 |
| 45 | √2/2 | √2/2 | 1 |
| 60 | √3/2 | 1/2 | √3 |
| 90 | 1 | 0 | 未定义 |
特殊角度的值及记忆技巧
30°、45°、60° 是三角函数中常用的特殊角度,其值具有规律性,便于记忆。
- 30°:sin=1/2,cos=√3/2,tan=√3/3。
- 45°:sin=cos=√2/2,tan=1。
- 60°:sin=√3/2,cos=1/2,tan=√3。
记忆口诀:
- 0°到90°:sin递增,cos递减,tan递增。
- 特殊角度:30°、45°、60°是记忆的关键点。
三角函数值的几何意义
- sinθ:在单位圆中,θ角的正弦值等于其终边与单位圆交点的y坐标。
- cosθ:等于交点的x坐标。
- tanθ:等于sinθ/cosθ,即y/x。
通过单位圆可以直观理解三角函数的周期性和对称性。
应用示例
假设有一个直角三角形,其中一个锐角为30°,斜边长度为2,则对边长度为1,邻边长度为√3。
- sin30° = 对边/斜边 = 1/2
- cos30° = 邻边/斜边 = √3/2
- tan30° = 对边/邻边 = 1/√3 = √3/3
掌握0°到90°的三角函数值表是学习三角函数的基础,通过理解其几何意义、记忆特殊角度的值,并结合实际应用,可以更好地掌握这一重要数学工具,希望本文能为你的学习提供帮助!
如需更详细的三角函数表或扩展内容(如90°到360°),欢迎继续提问!
相关文章:
文章已关闭评论!