反三角函数值对照表全部:反三角函数值对照表(完整版)
反三角函数是三角函数的逆运算,主要包括 arcsin(反正弦)、arccos(反余弦)、arctan(反正切) 及其反函数,它们在数学、物理、工程等领域有广泛应用,本文将提供完整的反三角函数值对照表,并附上相关说明,帮助读者快速掌握这些函数的值。
反三角函数定义回顾
反正弦函数(arcsin)
- 定义域:([-1, 1])
- 值域:([-\frac{\pi}{2}, \frac{\pi}{2}])
- 函数关系:若 (\sin y = x),则 (y = \arcsin x)。
反余弦函数(arccos)
- 定义域:([-1, 1])
- 值域:([0, \pi])
- 函数关系:若 (\cos y = x),则 (y = \arccos x)。
反正切函数(arctan)
- 定义域:((-\infty, +\infty))
- 值域:((-\frac{\pi}{2}, \frac{\pi}{2}))
- 函数关系:若 (\tan y = x),则 (y = \arctan x)。
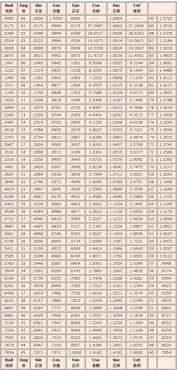
反三角函数值对照表
以下是常见角度(以弧度表示)对应的反三角函数值,精确到小数点后四位:

| 角度(弧度) | (\arcsin x) | (\arccos x) | (\arctan x) |
|---|---|---|---|
| (0) | (0) | (\frac{\pi}{2}) | (0) |
| (\frac{\pi}{6}) | (\frac{\pi}{6}) | (\frac{5\pi}{6}) | (\frac{\pi}{6}) |
| (\frac{\pi}{4}) | (\frac{\pi}{4}) | (\frac{3\pi}{4}) | (\frac{\pi}{4}) |
| (\frac{\pi}{3}) | (\frac{\pi}{3}) | (\frac{2\pi}{3}) | (\frac{\pi}{3}) |
| (\frac{\pi}{2}) | (\frac{\pi}{2}) | (0) | 未定义 |
| (-\frac{\pi}{6}) | (-\frac{\pi}{6}) | (\frac{7\pi}{6}) | (-\frac{\pi}{6}) |
| (-\frac{\pi}{4}) | (-\frac{\pi}{4}) | (\frac{3\pi}{4}) | (-\frac{\pi}{4}) |
| (-\frac{\pi}{3}) | (-\frac{\pi}{3}) | (\frac{4\pi}{3}) | (-\frac{\pi}{3}) |
| (1) | (\arcsin(1) = \frac{\pi}{2}) | (\arccos(1) = 0) | (\arctan(1) = \frac{\pi}{4}) |
| (-1) | (\arcsin(-1) = -\frac{\pi}{2}) | (\arccos(-1) = \pi) | (\arctan(-1) = -\frac{\pi}{4}) |
注:表格中 (x) 为输入值,(y) 为输出值。(\arcsin(0.5) = \frac{\pi}{6})。
反三角函数的图像与性质
图像特点

- arcsin:单调递增,图像关于原点对称(奇函数)。
- arccos:单调递减,图像关于 (y = \frac{\pi}{2}) 对称(非奇非偶)。
- arctan:单调递增,图像关于原点对称(奇函数)。
常见关系式
- (\arcsin x + \arccos x = \frac{\pi}{2})
- (\arctan x + \arctan \frac{1}{x} = \frac{\pi}{2})(当 (x > 0) 时)
应用示例
求解三角方程
例:(\sin y = \frac{\sqrt{3}}{2}),则 (y = \arcsin(\frac{\sqrt{3}}{2}) = \frac{\pi}{3})。
几何问题
- 例:已知直角三角形的邻边为 3,斜边为 5,求锐角 (\theta):
(\cos \theta = \frac{3}{5}),则 (\theta = \arccos(\frac{3}{5}))。
- 例:已知直角三角形的邻边为 3,斜边为 5,求锐角 (\theta):
记忆技巧
- 口诀记忆:对于特殊角度(如 (\frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{3})),可以通过单位圆或三角形边角关系快速记忆。
- 图像辅助:绘制反三角函数图像,观察其变化趋势,有助于理解函数性质。
相关文章:
文章已关闭评论!