初等函数定义：初等函数的定义与分类

初等函数的定义与分类

在数学分析中,初等函数是数学中最基本、应用最广泛的函数类型之一，它们构成了许多复杂函数的基础，并在科学、工程、经济等领域中广泛使用，初等函数的定义不仅为函数的分类提供了依据，也为后续的极限、导数、积分等概念的讨论奠定了基础，本文将从初等函数的定义出发，探讨其分类、性质及应用。

初等函数的定义

初等函数是指由常数、变量以及基本运算（加、减、乘、除、乘方、开方）和基本初等函数（幂函数、指数函数、对数函数、三角函数、反三角函数）通过有限次组合而成的函数，初等函数包括以下几类：

1. 常数函数：形式为 ( f(x) = c )，( c ) 是常数。
2. 幂函数：形式为 ( f(x) = x^a )，( a ) 是常数。
3. 指数函数：形式为 ( f(x) = a^x )，( a > 0 ) 且 ( a \neq 1 )。
4. 对数函数：形式为 ( f(x) = \log_a x )，( a > 0 ) 且 ( a \neq 1 )。
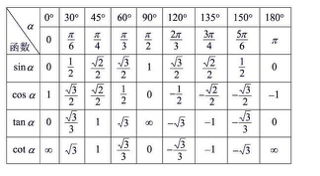
5. 三角函数：如 ( \sin x )、( \cos x )、( \tan x ) 等。
6. 反三角函数：如 ( \arcsin x )、( \arccos x )、( \arctan x ) 等。
7. 复合函数：由两个或多个初等函数通过复合运算得到的函数。
8. 初等函数的组合：包括加、减、乘、除等运算得到的函数。

初等函数的定义强调了其“初等性”，即通过有限次的基本运算和基本初等函数组合而成，不包括特殊函数（如伽马函数、贝塞尔函数等）。

初等函数的分类

根据其表达式和性质,初等函数可以进一步分为以下几类：

1. 代数函数：包括常数函数、幂函数、有理函数（多项式函数和有理函数）等，代数函数满足某个代数方程，其表达式仅包含有限次的加、减、乘、除和乘方运算。

2. 超越函数：包括指数函数、对数函数、三角函数及其反函数等，超越函数不满足任何有理系数的代数方程，其表达式涉及超越运算（如指数、对数、三角等）。

3. 复合函数：由两个或多个函数通过复合运算得到的函数。( f(x) = \sin(x^2) ) 是复合函数，其中外层函数是正弦函数，内层函数是幂函数。

4. 分段函数：在定义域的不同部分使用不同的表达式，符号函数 ( \text{sgn}(x) = \begin{cases} 1 & x > 0 \ 0 & x = 0 \ -1 & x < 0 \end{cases} ) 是一个分段函数。

初等函数的性质

初等函数具有许多重要的性质,这些性质在微积分和数学分析中起着关键作用：

1. 连续性：初等函数在其定义域内通常是连续的，除了某些特殊点（如分母为零的点、对数函数的定义域边界等）。

2. 可导性：初等函数在其定义域内通常是可导的，且导数仍为初等函数，幂函数的导数是幂函数，指数函数的导数是指数函数。

3. 单调性：某些初等函数（如指数函数、对数函数、幂函数）具有单调性，这在求解方程和不等式时非常有用。

4. 周期性：三角函数具有周期性，这一性质在周期现象的研究中具有重要意义。

初等函数的应用

初等函数在科学和工程中有着广泛的应用。

• 物理学：运动学中的位移、速度、加速度函数通常用初等函数表示。
• 经济学：需求函数、供给函数、成本函数等常常用初等函数建模。
• 工程学：电路分析、信号处理等领域广泛使用初等函数。
• 概率论：许多概率分布（如正态分布、指数分布）的密度函数是初等函数。

初等函数是数学分析的基础,其定义和分类为更复杂的函数研究提供了框架，理解初等函数的定义、分类、性质及其应用，不仅有助于掌握数学分析的基本概念，也为解决实际问题提供了有力的工具，在学习过程中，学生应注重对初等函数的深入理解和灵活应用，以提高数学素养和解决问题的能力。