初等函数的概念：初等函数的概念

初等函数是数学分析中的基本函数类型，它们由常数、变量以及基本的运算（如加、减、乘、除、乘方、开方）和基本初等函数通过有限次组合而成，初等函数是数学分析的基础，广泛应用于科学、工程和经济等领域,理解初等函数的概念对于掌握微积分及其应用至关重要。

初等函数的定义

初等函数通常包括以下几类：

1. 幂函数：形式为 ( f(x) = x^a )，( a ) 是常数。
2. 指数函数：形式为 ( f(x) = a^x )，( a > 0 ) 且 ( a \neq 1 )。
3. 对数函数：形式为 ( f(x) = \log_a x )，( a > 0 ) 且 ( a \neq 1 )。
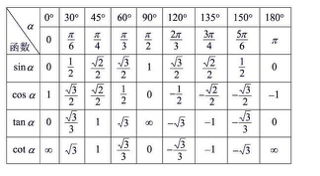
4. 三角函数：如正弦、余弦、正切等，( f(x) = \sin x )、( f(x) = \cos x )。
5. 反三角函数：如反正弦、反余弦、反正切等，( f(x) = \arcsin x )。
6. 双曲函数：如双曲正弦、双曲余弦等，( f(x) = \sinh x )、( f(x) = \cosh x )。

初等函数的性质

初等函数具有以下一些基本性质：

1. 连续性：初等函数在其定义域内通常是连续的。
2. 可导性：初等函数在其定义域内通常是可导的。
3. 单调性：某些初等函数（如指数函数、对数函数）具有单调性。
4. 周期性：三角函数具有周期性。

初等函数的组合

初等函数可以通过有限次的四则运算（加、减、乘、除）和复合运算得到更复杂的函数，函数 ( f(x) = \sin(x^2) ) 是由正弦函数和幂函数复合而成的初等函数。

初等函数的重要性

初等函数是数学分析的基础，它们在微积分、微分方程、傅里叶分析等领域中起着重要作用，通过研究初等函数的性质，可以解决许多实际问题，如物理学中的运动、生物学中的增长模型、经济学中的优化问题等。

初等函数是数学分析中的基本概念，理解它们的定义、性质和应用对于深入学习高等数学具有重要意义，通过掌握初等函数的基本知识,可以为后续学习更复杂的数学内容打下坚实的基础。