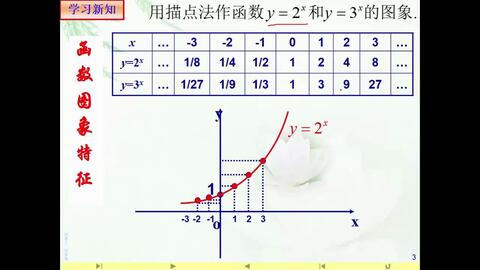
指数函数的求导公式：指数函数的求导公式及其应用

指数函数的求导公式

自然指数函数的求导

自然指数函数 ( e^x ) 的导数是其本身，即：

[ \frac{d}{dx} e^x = e^x ]

这一性质是指数函数求导的基础,也是其区别于其他函数的重要特征。

一般指数函数的求导

对于一般形式的指数函数 ( a^x )（( a > 0 ) 且 ( a \neq 1 )），其导数公式为：

[ \frac{d}{dx} a^x = a^x \ln a ]

( \ln a ) 是以自然对数为底的对数函数。

求导公式的推导

自然指数函数的推导

自然指数函数 ( e^x ) 的导数可以通过定义推导：

[ \frac{d}{dx} e^x = \lim{\Delta x \to 0} \frac{e^{x+\Delta x} - e^x}{\Delta x} = \lim{\Delta x \to 0} \frac{e^x (e^{\Delta x} - 1)}{\Delta x} = e^x \lim_{\Delta x \to 0} \frac{e^{\Delta x} - 1}{\Delta x} ]

根据极限定义,( \lim_{\Delta x \to 0} \frac{e^{\Delta x} - 1}{\Delta x} = 1 )，

[ \frac{d}{dx} e^x = e^x ]

一般指数函数的推导

对于 ( a^x )，可以将其转化为自然指数函数：

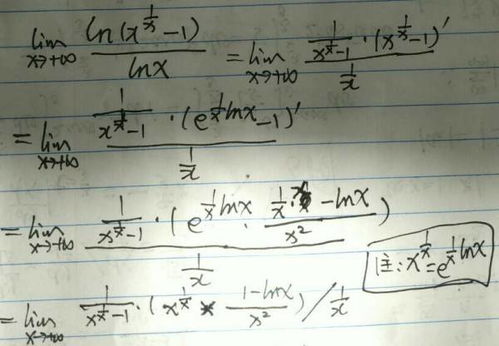
[ a^x = e^{x \ln a} ]

然后使用链式法则求导：

[ \frac{d}{dx} a^x = \frac{d}{dx} e^{x \ln a} = e^{x \ln a} \cdot \frac{d}{dx} (x \ln a) = a^x \cdot \ln a ]

一般指数函数的导数公式为 ( a^x \ln a )。

常见错误与注意事项

1. 底数 ( a ) 的限制：当 ( a = 1 ) 时，函数为常数函数，其导数为零；当 ( a = 0 ) 时，函数无定义。
2. 对数换底公式：在求导过程中，( \ln a ) 是以 ( e ) 为底的对数，若使用其他底数，需转换为自然对数。
3. 复合函数求导：当指数函数包含复合函数时，需使用链式法则。

应用示例

求 ( y = 3^x ) 的导数

[ \frac{dy}{dx} = 3^x \ln 3 ]

求 ( y = e^{2x} ) 的导数

[ \frac{dy}{dx} = e^{2x} \cdot 2 = 2e^{2x} ]

求 ( y = x^x ) 的导数

( y = x^x ) 可以写成 ( y = e^{x \ln x} )，然后求导：

[ \frac{dy}{dx} = e^{x \ln x} \cdot \frac{d}{dx} (x \ln x) = x^x \left( \ln x + 1 \right) ]

指数函数的求导公式是微积分中的基础内容,掌握其推导过程和应用方法对于解决更复杂的数学问题至关重要，无论是自然指数函数还是一般指数函数，其求导公式都有其特定的形式和推导方法，通过不断练习和应用，可以加深对这一公式的理解，提高解题能力。

参考文献：

• Stewart, J. (2021). Calculus: Early Transcendentals. Cengage Learning.
• Thomas, G. B. (2016). Thomas' Calculus. Pearson.