指数函数的性质：指数函数的性质，定义、图像与应用

指数函数的定义

指数函数的定义为：对于任意实数 ( x )，函数 ( f(x) = a^x ) 称为指数函数，( a ) 是底数，且 ( a > 0 ) 且 ( a \neq 1 )，当 ( a = 1 ) 时，函数恒等于 1，此时不再称为指数函数；当 ( a \leq 0 ) 时，函数在实数域上无定义或不连续，因此底数 ( a ) 必须为正且不等于 1。

指数函数的基本性质

1. 定义域与值域

   • 定义域：( (-\infty, +\infty) )
   • 值域：当 ( a > 1 ) 时，值域为 ( (0, +\infty) )；当 ( 0 < a < 1 ) 时，值域同样为 ( (0, +\infty) )。

2. 单调性

   • 当 ( a > 1 ) 时，函数 ( f(x) = a^x ) 是增函数，即 ( x_1 < x_2 ) 时，( f(x_1) < f(x_2) )。
   • 当 ( 0 < a < 1 ) 时，函数 ( f(x) = a^x ) 是减函数，即 ( x_1 < x_2 ) 时，( f(x_1) > f(x_2) )。

3. 过定点
   指数函数恒过点 ( (0, 1) )，因为 ( a^0 = 1 )（( a \neq 0 )）。

4. 极限性质

   • 当 ( x \to +\infty ) 时：
     • 若 ( a > 1 )，则 ( a^x \to +\infty )；
     • 若 ( 0 < a < 1 )，则 ( a^x \to 0 )。
   • 当 ( x \to -\infty ) 时：
     • 若 ( a > 1 )，则 ( a^x \to 0 )；
     • 若 ( 0 < a < 1 )，则 ( a^x \to +\infty )。

5. 特殊点

   • 当 ( x = 1 ) 时，( f(1) = a )；
   • 当 ( x = -1 ) 时，( f(-1) = \frac{1}{a} )。

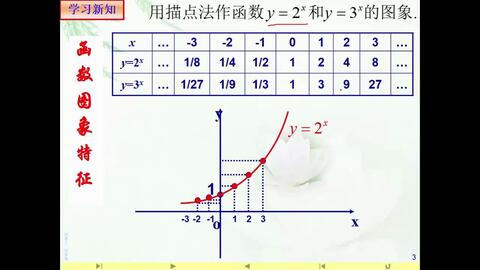
指数函数的图像特征

指数函数的图像具有以下特点：

• 底数 ( a > 1 )：图像从左到右逐渐上升，且过点 ( (0, 1) ) 和 ( (1, a) )。
• 底数 ( 0 < a < 1 )：图像从左到右逐渐下降，且同样过点 ( (0, 1) ) 和 ( (1, a) )。
• 图像对称性：函数 ( y = a^x ) 与 ( y = \left(\frac{1}{a}\right)^x ) y 轴对称。

指数函数的应用

1. 复利计算
   在金融领域，复利公式 ( A = P(1 + r)^t ) 中，( (1 + r)^t ) 就是指数函数，用于计算本金 ( P ) 在利率 ( r ) 下经过 ( t ) 年后的本息和 ( A )。

2. 放射性衰变
   物理学中，放射性元素的衰变规律可以用指数函数表示，如 ( N(t) = N_0 \cdot e^{-\lambda t} )，( N_0 ) 是初始原子数，( \lambda ) 是衰变常数。

3. 人口增长模型
   在生态学中，若人口增长率恒定，则人口数量随时间的变化可以用指数函数描述，如 ( P(t) = P_0 \cdot e^{rt} )，( P_0 ) 是初始人口，( r ) 是增长率。

4. 其他应用
   指数函数还广泛应用于化学反应速率、生物医学、信号处理等领域。

常见误区与注意事项

• 底数 ( a ) 必须大于 0 且不等于 1：若 ( a \leq 0 )，函数在实数域上无定义或不连续。
• 指数函数与幂函数的区别：指数函数的变量在指数位置，而幂函数的变量在底数位置。
• 单调性取决于底数：当 ( a > 1 ) 时递增，当 ( 0 < a < 1 ) 时递减。