6种三角函数图像与性质：六种三角函数图像与性质全解析，从基础到应用

六种三角函数的定义

在单位圆（半径为1的圆）中，设角θ的终边与单位圆交于点P(x, y),则：

• 正弦函数：sinθ = y
• 余弦函数：cosθ = x
• 正切函数：tanθ = y/x（x≠0）
• 余切函数：cotθ = x/y（y≠0）
• 正割函数：secθ = 1/x（x≠0）
• 余割函数：cscθ = 1/y（y≠0）

这六种函数是相互关联的，例如tanθ = sinθ/cosθ，secθ = 1/cosθ，cscθ = 1/sinθ，cotθ = cosθ/sinθ。

图像与性质分析

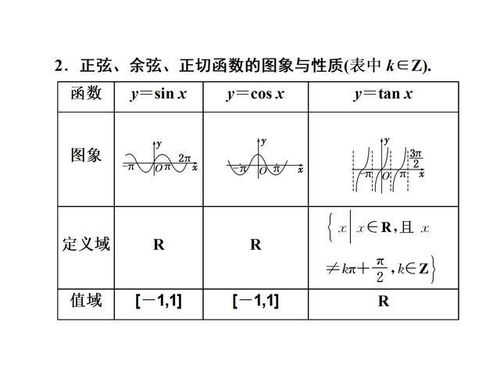
正弦函数：y = sinθ

• 图像：正弦函数的图像是一个周期为2π的波形曲线，从原点出发，向上凸起，向下凹陷，每2π重复一次。
• 性质：
  • 定义域：全体实数
  • 值域：[-1, 1]
  • 周期：2π
  • 奇函数：sin(-θ) = -sinθ
  • 单调性：在[-π/2 + 2kπ, π/2 + 2kπ]上单调递增，在[π/2 + 2kπ, 3π/2 + 2kπ]上单调递减
  • 对称性：关于原点对称
  • 零点：θ = kπ（k为整数）
  • 最大值：θ = π/2 + 2kπ，y=1
  • 最小值：θ = 3π/2 + 2kπ，y=-1

余弦函数：y = cosθ

• 图像：余弦函数的图像是一个周期为2π的波形曲线，从(0,1)出发，向右下降，向左上升，每2π重复一次。
• 性质：
  • 定义域：全体实数
  • 值域：[-1, 1]
  • 周期：2π
  • 偶函数：cos(-θ) = cosθ
  • 单调性：在[-π + 2kπ, 2kπ]上单调递增，在[2kπ, π + 2kπ]上单调递减
  • 对称性：关于y轴对称
  • 零点：θ = π/2 + kπ（k为整数）
  • 最大值：θ = 2kπ，y=1
  • 最小值：θ = π + 2kπ，y=-1

正切函数：y = tanθ

• 图像：正切函数的图像是一个周期为π的曲线，图像在每个周期内穿过原点，且在θ = π/2 + kπ处有垂直渐近线。
• 性质：
  • 定义域：θ ≠ π/2 + kπ（k为整数）
  • 值域：全体实数
  • 周期：π
  • 奇函数：tan(-θ) = -tanθ
  • 单调性：在(-π/2 + kπ, π/2 + kπ)上单调递增
  • 对称性：关于原点对称
  • 零点：θ = kπ（k为整数）
  • 渐近线：θ = π/2 + kπ

余切函数：y = cotθ

• 图像：余切函数的图像是一个周期为π的曲线，图像在每个周期内穿过原点，且在θ = kπ处有垂直渐近线。
• 性质：
  • 定义域：θ ≠ kπ（k为整数）
  • 值域：全体实数
  • 周期：π
  • 奇函数：cot(-θ) = -cotθ
  • 单调性：在(kπ, π + kπ)上单调递减
  • 对称性：关于原点对称
  • 零点：θ = π/2 + kπ（k为整数）
  • 渐近线：θ = kπ

正割函数：y = secθ

• 图像：正割函数的图像是一个周期为2π的曲线，图像在每个周期内有两个波峰和两个波谷，且在θ = π/2 + kπ处有垂直渐近线。
• 性质：
  • 定义域：θ ≠ π/2 + kπ（k为整数）
  • 值域：(-∞, -1] ∪ [1, +∞)
  • 周期：2π
  • 偶函数：sec(-θ) = secθ
  • 单调性：在[2kπ - π/2, 2kπ + π/2]上单调递减
  • 对称性：关于y轴对称
  • 零点：无
  • 最大值：θ = 2kπ，y=1
  • 最小值：θ = π + 2kπ，y=-1
  • 渐近线：θ = π/2 + kπ

余割函数：y = cscθ

• 图像：余割函数的图像是一个周期为2π的曲线，图像在每个周期内有两个波峰和两个波谷，且在θ = kπ处有垂直渐近线。
• 性质：
  • 定义域：θ ≠ kπ（k为整数）
  • 值域：(-∞, -1] ∪ [1, +∞)
  • 周期：2π
  • 奇函数：csc(-θ) = -cscθ
  • 单调性：在[kπ - π/2, kπ + π/2]上单调递减
  • 对称性：关于原点对称
  • 零点：无
  • 最大值：θ = π/2 + 2kπ，y=1
  • 最小值：θ = 3π/2 + 2kπ，y=-1
  • 渐近线：θ = kπ

六种三角函数的图像与性质各有特点，但它们之间存在密切的联系，正切函数是正弦函数与余弦函数的比值，正割函数是余弦函数的倒数，理解这些函数的图像和性质，不仅有助于解决数学问题，还能为后续学习微积分、傅里叶变换等高级内容打下坚实基础。

在实际应用中，三角函数广泛用于描述周期性现象，如声波、光波、简谐运动等，掌握其图像与性质,能够帮助我们更好地分析和解决实际问题。