正切函数和差公式：正切函数和差公式的完全解析与应用示例

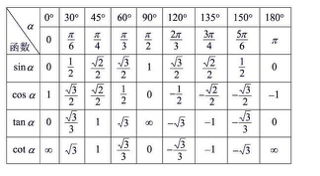
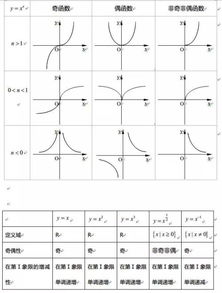
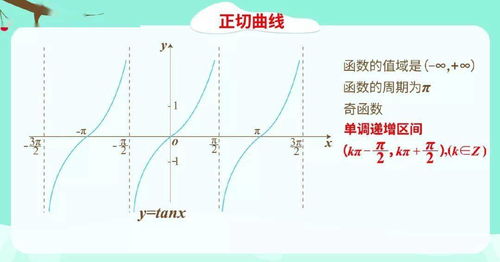
正切函数的定义与图像

正切函数（Tangent Function），通常用符号 (\tan \theta) 表示，是三角函数的一种，它的定义为：
[ \tan \theta = \frac{\sin \theta}{\cos \theta} ]
(\sin \theta) 是角 (\theta) 的正弦值，(\cos \theta) 是角 (\theta) 的余弦值。
正切函数的图像是一条周期为 (\pi) 的函数图像，具有无限多个垂直渐近线，渐近线的位置为 (\theta = \frac{\pi}{2} + k\pi)（(k) 为整数）。

正切函数的和差公式

正切函数的和差公式是三角函数中非常重要的公式之一,用于计算两个角的和或差的正切值，其公式如下：

和角公式：
[ \tan(\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta} ]

差角公式：
[ \tan(\alpha - \beta) = \frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta} ]

推导过程：
根据正切函数的定义，结合正弦和余弦的和角公式：
[ \sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta ]
[ \cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta ]
则：
[ \tan(\alpha + \beta) = \frac{\sin(\alpha + \beta)}{\cos(\alpha + \beta)} = \frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta - \sin \alpha \sin \beta} ]
分子分母同时除以 (\cos \alpha \cos \beta)：
[ \tan(\alpha + \beta) = \frac{\frac{\sin \alpha}{\cos \alpha} + \frac{\sin \beta}{\cos \beta}}{1 - \frac{\sin \alpha}{\cos \alpha} \cdot \frac{\sin \beta}{\cos \beta}} = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta} ]
差角公式的推导类似，只需将 (\beta) 替换为 (-\beta)，并利用 (\tan(-\beta) = -\tan \beta) 即可。

公式应用示例

例1：计算 (\tan(75^\circ))
已知 (75^\circ = 45^\circ + 30^\circ)，则：
[ \tan(75^\circ) = \tan(45^\circ + 30^\circ) = \frac{\tan 45^\circ + \tan 30^\circ}{1 - \tan 45^\circ \tan 30^\circ} ]
代入 (\tan 45^\circ = 1)，(\tan 30^\circ = \frac{\sqrt{3}}{3})：
[ \tan(75^\circ) = \frac{1 + \frac{\sqrt{3}}{3}}{1 - 1 \cdot \frac{\sqrt{3}}{3}} = \frac{\frac{3 + \sqrt{3}}{3}}{\frac{3 - \sqrt{3}}{3}} = \frac{3 + \sqrt{3}}{3 - \sqrt{3}} ]
分子分母同时乘以 (3 + \sqrt{3})（分母的共轭）：
[ \tan(75^\circ) = \frac{(3 + \sqrt{3})^2}{(3)^2 - (\sqrt{3})^2} = \frac{9 + 6\sqrt{3} + 3}{9 - 3} = \frac{12 + 6\sqrt{3}}{6} = 2 + \sqrt{3} ]

例2：化简 (\tan(\alpha - \beta))
若 (\alpha = 60^\circ)，(\beta = 30^\circ)，则：
[ \tan(30^\circ) = \tan(60^\circ - 30^\circ) = \frac{\tan 60^\circ - \tan 30^\circ}{1 + \tan 60^\circ \tan 30^\circ} ]
代入 (\tan 60^\circ = \sqrt{3})，(\tan 30^\circ = \frac{\sqrt{3}}{3})：
[ \tan(30^\circ) = \frac{\sqrt{3} - \frac{\sqrt{3}}{3}}{1 + \sqrt{3} \cdot \frac{\sqrt{3}}{3}} = \frac{\frac{3\sqrt{3} - \sqrt{3}}{3}}{\frac{3 + 3}{3}} = \frac{\frac{2\sqrt{3}}{3}}{\frac{6}{3}} = \frac{2\sqrt{3}}{3} \times \frac{1}{2} = \frac{\sqrt{3}}{3} ]
结果与已知值一致。

常见错误与注意事项

1. 分母不能为零：在使用和差公式时，需确保分母 (1 - \tan \alpha \tan \beta \neq 0)，否则公式不适用。
2. 角度范围：公式适用于任意角度，但需注意角度的周期性。
3. 记忆技巧：可通过对比正弦和余弦的和差公式，记忆正切公式的分子分母结构。

正切函数的和差公式是三角函数中的核心工具之一,广泛应用于数学、物理、工程等领域，掌握其推导过程和应用方法，能够帮助我们更灵活地解决与角度运算相关的问题，通过不断练习和实际应用，可以加深对公式的理解和记忆。