求极限等于求导吗：求极限与求导，不可混为一谈的数学概念

极限的定义与意义

极限是微积分中的核心概念，它描述了函数在某一点附近的行为趋势，如果当自变量趋近于某一点时，函数值无限趋近于某个确定的值,那么这个确定的值就是函数在该点的极限。

考虑函数 ( f(x) = \frac{x^2 - 1}{x - 1} )，当 ( x ) 趋近于 1 时，函数的值趋近于 2，

[ \lim_{x \to 1} \frac{x^2 - 1}{x - 1} = 2 ]

极限的计算通常通过直接代入、因式分解、洛必达法则等方法完成，其目标是确定函数在某点的“行为趋势”。

导数的定义与意义

导数是函数在某一点处的瞬时变化率，它描述了函数图像在该点的切线斜率,导数的定义基于极限：

[ f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} ]

这个极限表示当自变量的变化量 ( \Delta x ) 趋近于 0 时，函数值的变化量与自变量变化量的比值的极限，如果这个极限存在，则称函数在该点可导,且该极限值就是导数值。

函数 ( f(x) = x^2 ) 的导数为：

[ f'(x) = \lim{\Delta x \to 0} \frac{(x + \Delta x)^2 - x^2}{\Delta x} = \lim{\Delta x \to 0} \frac{2x\Delta x + (\Delta x)^2}{\Delta x} = 2x ]

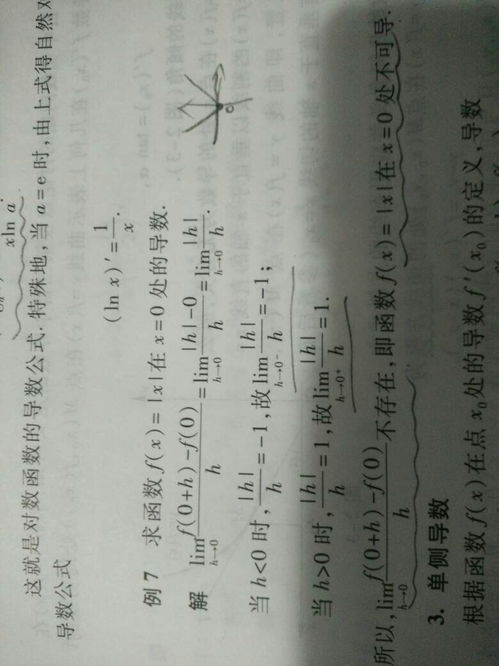
导数的计算通常依赖于极限,但并非所有极限都能转化为导数。

求极限与求导的区别

1. 定义不同
   极限是函数在某点的“行为趋势”，而导数是函数在某点的“瞬时变化率”。

2. 计算方法不同
   求极限的方法包括直接代入、因式分解、洛必达法则等；求导则需要使用导数定义或求导法则（如幂法则、乘积法则、链式法则等）。

3. 结果意义不同
   极限的结果是一个数值或符号（如无穷大），而导数的结果是一个函数（导函数）,表示函数在任意点的瞬时变化率。

   

4. 存在条件不同
   函数在某点可导必须满足两个条件：

   • 函数在该点连续；
   • 函数在该点的左右导数存在且相等。

常见误区与澄清

许多学生误以为“求导就是求极限”，或者“求极限等于求导”，这种理解是片面的，虽然导数的定义依赖于极限,但两者并非同一概念。

• 函数 ( f(x) = |x| ) 在 ( x = 0 ) 处的极限存在（为 0），但导数不存在,因为左右导数不相等。

• 函数 ( f(x) = \frac{1}{x} ) 在 ( x = 0 ) 处的极限不存在（趋向无穷大）,因此也无法求导。

求极限与求导是微积分中两个独立但又相互关联的概念，极限是导数的基础，但并非所有极限都能转化为导数，反之亦然，理解两者的区别对于掌握微积分的核心思想至关重要，在实际应用中，极限用于分析函数的长期行为,而导数则用于研究函数的瞬时变化。

希望本文能帮助读者在学习微积分时更加清晰地区分“求极限”与“求导”这两个关键概念。