三角函数正弦余弦表:三角函数正弦余弦表,从定义到记忆方法
正弦和余弦的定义
在单位圆(半径为1的圆)中,任意角度θ的正弦值(sinθ)等于该角度对应的点的y坐标,余弦值(cosθ)等于该点的x坐标,当θ=0°时,点坐标为(1,0),因此cos0°=1,sin0°=0。
正弦和余弦的定义也可以通过直角三角形表示:
- sinθ = 对边 / 斜边
- cosθ = 邻边 / 斜边
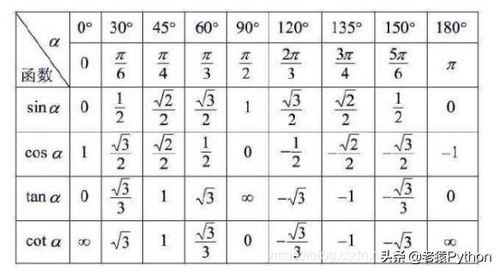
常见角度的正弦余弦值表
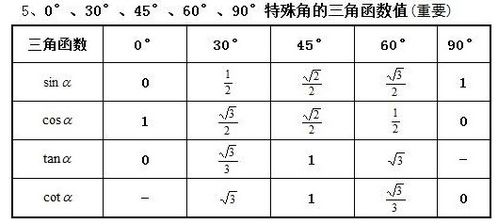
以下是0°到90°之间常见角度的正弦和余弦值,这些角度在三角函数学习中非常重要:
| 角度(°) | 正弦(sin) | 余弦(cos) |
|---|---|---|
| 0° | 0 | 1 |
| 30° | 1/2 | √3/2 |
| 45° | √2/2 | √2/2 |
| 60° | √3/2 | 1/2 |
| 90° | 1 | 0 |
说明:

- 30°、45°、60°是三角函数中常用的特殊角,其值可以通过几何方法(如等边三角形、直角等腰三角形)推导得出。
- 180°及以上的角度可以通过诱导公式转换为0°到90°之间的角度计算。
记忆方法
口诀法
对于特殊角的正弦值,可以使用以下口诀:- 30°:sin=1/2
- 45°:sin=√2/2
- 60°:sin=√3/2
记忆时可以联想“一、二、三”,分别对应分子为1、√2、√3。
对称性与诱导公式
- sin(180°-θ)=sinθ
- cos(180°-θ)=-cosθ
通过这些公式,可以将其他角度的值转化为特殊角的值。
单位圆法
在单位圆上,特殊角的终边与圆的交点坐标可以直接写出正弦和余弦值,30°:点坐标为(√3/2, 1/2),因此cos30°=√3/2,sin30°=1/2。
应用场景
正弦和余弦表在以下场景中非常实用:
- 几何问题:计算三角形的边长或角度。
- 物理问题:分析简谐运动、波动和力的分解。
- 工程计算:用于信号处理、建筑和机械设计。
相关文章:
文章已关闭评论!