三角函数表格0到360：掌握0°到360°三角函数值表与记忆技巧

三角函数是数学中描述角度与直角三角形边长关系的基本函数,包括正弦(sin)、余弦(cos)和正切(tan)等，在学习和应用数学、物理等领域时，快速准确地获取特定角度的三角函数值至关重要，本文将重点介绍0°到360°范围内常用特殊角度的三角函数值表，并提供一些记忆这些值的技巧。

0°到360°三角函数值表

以下是0°到360°之间一些关键特殊角度（0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°）的正弦(sin)、余弦(cos)和正切(tan)值，这些角度是学习三角函数的基础，其函数值具有规律性。

| 角度 (°) | 弧度 (rad) | sin(θ) | cos(θ) | tan(θ) | | ：------- | :--------- | :----- | :----- | :----- | | 0 | 0 | 0 | 1 | 0 | | 30 | π/6 | 1/2 | √3/2 | √3/3 | | 45 | π/4 | √2/2 | √2/2 | 1 | | 60 | π/3 | √3/2 | 1/2 | √3 | | 90 | π/2 | 1 | 0 | 无定义 | | 120 | 2π/3 | √3/2 | -1/2 | -√3 | | 135 | 3π/4 | √2/2 | -√2/2 | -1 | | 150 | 5π/6 | 1/2 | -√3/2 | -√3/3 | | 180 | π | 0 | -1 | 0 | | 210 | 7π/6 | -1/2 | -√3/2 | √3/3 | | 225 | 5π/4 | -√2/2 | -√2/2 | 1 | | 240 | 4π/3 | -√3/2 | -1/2 | √3 | | 270 | 3π/2 | -1 | 0 | 无定义 | | 300 | 5π/3 | -√3/2 | 1/2 | -√3 | | 315 | 7π/4 | -√2/2 | √2/2 | -1 | | 330 | 11π/6 | -1/2 | √3/2 | -√3/3 | | 360 | 2π | 0 | 1 | 0 |

如何使用这个表格

1. 查找特定角度的函数值： 直接在表格中找到对应的角度，即可读取其sin、cos或tan值。
2. 理解周期性： 三角函数是周期函数，sin(θ)和cos(θ)的周期是360°，tan(θ)的周期是180°，这意味着sin(θ + 360°k) = sin(θ)，cos(θ + 360°k) = cos(θ)，tan(θ + 180°k) = tan(θ)，其中k是任意整数，0°到360°的表格实际上包含了所有角度的信息。
3. 理解象限： 角度所在的象限决定了sin、cos、tan值的符号。
   • 第一象限 (0°-90°)：sin、cos、tan均为正。
   • 第二象限 (90°-180°)：sin为正，cos、tan为负。
   • 第三象限 (180°-270°)：sin、cos为负，tan为正。
   • 第四象限 (270°-360°)：sin为负，cos为正，tan为负。 观察表格可以清晰地看到这一规律。

记忆技巧

对于0°到360°的所有角度，全部记忆是不现实的，但以下方法可以帮助你更有效地记忆关键特殊角度的值：

1. 特殊角的记忆：

   • 0°, 90°, 180°, 270°, 360°： 这些是轴线角度，sin和cos值很容易记忆：0°和90°是1和0的组合，180°和270°是0和-1或-0的组合，360°回到0。
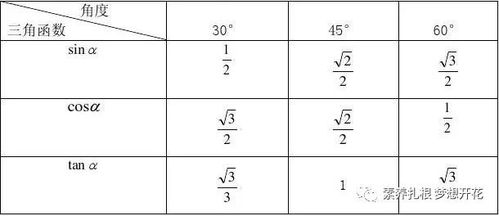
   • 30°, 45°, 60°： 这是核心特殊角。
     • sin值： 0°, 30°, 45°, 60°, 90°的sin值分别是 0, 0.5, √2/2≈0.707, √3/2≈0.866, 1，可以想象一个直角三角形，30°角的对边是斜边的一半，45°角的对边是邻边，60°角的对边是√3/2。
     • cos值： 由于sin²θ + cos²θ = 1，一旦记住了sin值，cos值可以通过开方和符号确定，或者，cos(θ) = sin(90°-θ)，这有助于记忆。
     • tan值： tan(θ) = sin(θ)/cos(θ)，或者记住tan(45°)=1，tan(30°)=√3/3，tan(60°)=√3。

2. 利用诱导公式：

   • 参考角： 任何角度都可以找到一个在0°到90°之间的“参考角”。
   • 诱导公式： 根据角度所在的象限，可以使用诱导公式将任意角度的三角函数值转化为其参考角的三角函数值，并根据象限调整符号。
     • sin(180°-θ) = sin(θ)
     • sin(180°+θ) = -sin(θ)
     • sin(360°-θ) = -sin(θ) 或 sin(θ + 360°) = sin(θ)
     • cos(180°-θ) = -cos(θ)
     • cos(180°+θ) = -cos(θ)
     • cos(360°-θ) = cos(θ) 或 cos(θ + 360°) = cos(θ)
     • tan(180°-θ) = -tan(θ)
     • tan(180°+θ) = tan(θ)
     • tan(360°-θ) = -tan(θ) 或 tan(θ + 360°) = tan(θ) 掌握这些公式，你可以从0°到90°的值推导出其他所有象限的值。

3. 单位圆： 将角度放在单位圆上思考，点的坐标(x, y)即为(cosθ, sinθ)，想象单位圆上这些特殊点的位置，有助于直观理解和记忆。

掌握0°到360°的三角函数值表是学习三角函数的基础，虽然记忆所有值有困难，但通过理解特殊角、利用诱导公式和单位圆的概念，可以大大提高记忆效率和应用能力，上面提供的表格是您学习和解题时的有力工具，理解比死记硬背更重要，灵活运用这些知识才能真正掌握三角函数。