cot csc sec之间转换：三角函数 cot、csc、sec 之间的转换关系

基本定义

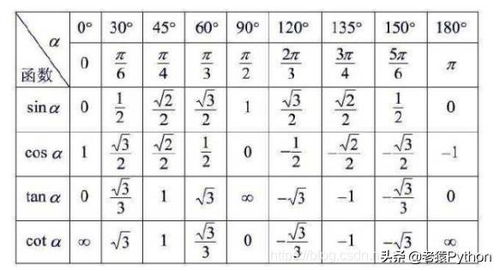
回顾一下这些函数的定义：

• 余切函数（cot）：cot(θ) = cos(θ) / sin(θ)
• 余割函数（csc）：csc(θ) = 1 / sin(θ)
• 正割函数（sec）：sec(θ) = 1 / cos(θ)

这些函数都是基于正弦和余弦函数定义的。

cot、csc、sec 之间的转换关系

cot 与 csc 的转换

cot(θ) 和 csc(θ) 都与 sin(θ) 有关，根据定义：

cot(θ) = cos(θ) / sin(θ)

csc(θ) = 1 / sin(θ)

cot(θ) 可以表示为：

cot(θ) = cos(θ) × csc(θ)

或者,通过三角恒等式：

cot²(θ) + 1 = csc²(θ)

这个恒等式是 cot 和 csc 之间的重要关系。

cot 与 sec 的转换

cot(θ) 和 sec(θ) 都与 cos(θ) 有关：

cot(θ) = cos(θ) / sin(θ)

sec(θ) = 1 / cos(θ)

cot(θ) 可以表示为：

cot(θ) = cos(θ) × csc(θ) = sec(θ) × cos²(θ)

或者,通过恒等式：

cot²(θ) + 1 = csc²(θ)

而 sec²(θ) = 1 + tan²(θ)

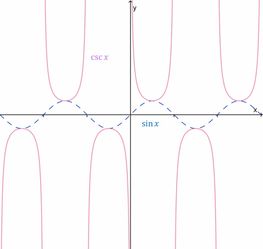
csc 与 sec 的转换

csc(θ) 和 sec(θ) 都是基于 sin(θ) 和 cos(θ) 的倒数，它们之间的转换关系可以通过以下恒等式实现：

csc(θ) = 1 / sin(θ)

sec(θ) = 1 / cos(θ)

csc(θ) 和 sec(θ) 之间没有直接的转换关系，但可以通过 sin(θ) 和 cos(θ) 的关系间接转换。

应用示例

假设有一个角度 θ，已知 sin(θ) = 1/2，求 cot(θ) 和 csc(θ)。

csc(θ) = 1 / sin(θ) = 1 / (1/2) = 2

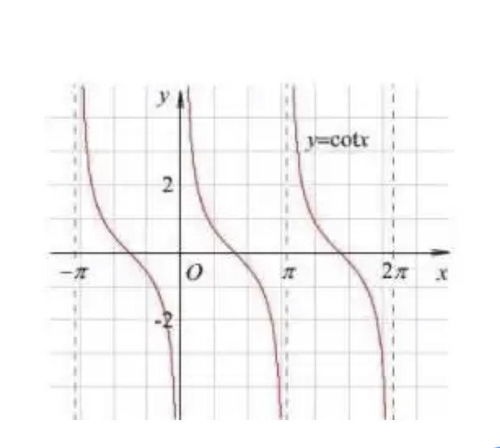
cot(θ) = cos(θ) / sin(θ)

根据 sin²(θ) + cos²(θ) = 1，可得：

cos²(θ) = 1 - sin²(θ) = 1 - (1/2)² = 1 - 1/4 = 3/4

cos(θ) = √(3/4) = √3/2（假设 θ 在第一象限）

cot(θ) = (√3/2) / (1/2) = √3

也可以使用恒等式 cot²(θ) + 1 = csc²(θ)：

cot²(θ) = csc²(θ) - 1 = 4 - 1 = 3

cot(θ) = √3（取正值）

cot、csc、sec 之间的转换关系主要基于三角函数的定义和恒等式，掌握这些关系有助于在解题过程中灵活运用三角函数，简化计算过程，在实际应用中，这些转换关系在积分、微分、几何问题中都有广泛的应用。

通过本文的介绍,相信读者对 cot、csc、sec 之间的转换关系有了更深入的理解。