三角函数sin cos tan对应的边：三角函数sin、cos、tan对应的边

在学习三角函数时,我们常常会遇到sin、cos、tan这三个基本函数，它们在几何学中与直角三角形的边长有着密切的关系，理解这些函数与三角形边长的对应关系，是掌握三角函数的基础。

直角三角形的边

在直角三角形中,我们有三条边：斜边、对边和邻边。

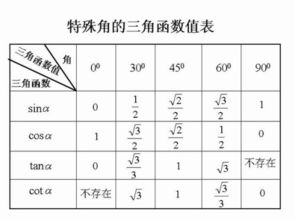
• 斜边：直角三角形中，与直角相对的边，是最长的一条边。
• 对边：与指定角（非直角）相对的边。
• 邻边：与指定角相邻的边，且不是斜边。

三角函数的定义

1. 正弦（sin）
   正弦函数对应的是指定角的对边与斜边的比值。
   [ \sin(\theta) = \frac{\text{对边}}{\text{斜边}} ]

2. 余弦（cos）
   余弦函数对应的是指定角的邻边与斜边的比值。
   [ \cos(\theta) = \frac{\text{邻边}}{\text{斜边}} ]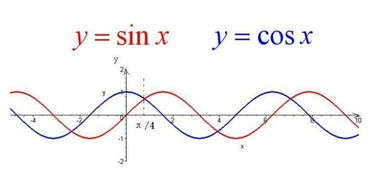

   

3. 正切（tan）
   正切函数对应的是指定角的对边与邻边的比值。
   [ \tan(\theta) = \frac{\text{对边}}{\text{邻边}} ]

三角函数与边的关系

通过上述定义可以看出,sin、cos、tan分别对应了直角三角形中不同的边长比例：

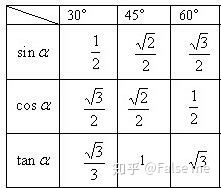
• sin：关注对边与斜边的关系。
• cos：关注邻边与斜边的关系。
• tan：关注对边与邻边的关系。

这些关系在几何学和物理学中有着广泛的应用,例如在测量高度、计算距离等问题中，我们常常需要利用三角函数来求解未知量。

记忆口诀

为了方便记忆,我们可以使用以下口诀：

SOH CAH TOA

• Sin = Opposite / Hypotenuse
• Cos = Adjacent / Hypotenuse
• Tan = Opposite / Adjacent

这个口诀可以帮助你快速回忆起sin、cos、tan对应的边。

三角函数sin、cos、tan与直角三角形的边长关系是三角学的基础，理解这些关系，不仅有助于掌握三角函数的定义，还能为后续学习打下坚实的基础，通过不断练习和应用，你将能够灵活运用这些函数解决实际问题。