正弦余弦正切：正弦、余弦、正切，三角函数的奥秘

正弦（sin）

正弦函数是直角三角形中对边与斜边之比的推广,在直角三角形中，一个锐角的正弦值等于其对边长度与斜边长度的比值，用数学符号表示为：

[ \sin \theta = \frac{\text{对边}}{\text{斜边}} ]

在单位圆（半径为1的圆）中，角θ的正弦值等于该角终边与单位圆交点的纵坐标，当θ=0°时，sin0°=0；当θ=90°时，sin90°=1。

正弦函数具有周期性,其周期为360°（或2π弧度），且是奇函数，即sin(-θ) = -sinθ。

余弦（cos）

余弦函数是直角三角形中邻边与斜边之比的推广,在直角三角形中，一个锐角的余弦值等于其邻边长度与斜边长度的比值，用数学符号表示为：

[ \cos \theta = \frac{\text{邻边}}{\text{斜边}} ]

在单位圆中,角θ的余弦值等于该角终边与单位圆交点的横坐标，当θ=0°时，cos0°=1；当θ=90°时，cos90°=0。

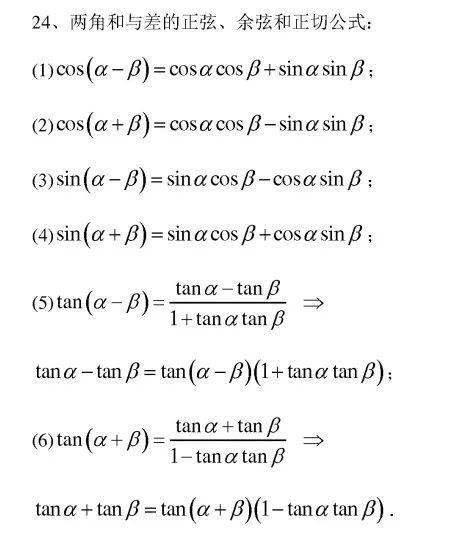
余弦函数同样具有周期性,周期为360°，且是偶函数，即cos(-θ) = cosθ。

正切（tan）

正切函数是正弦与余弦之比的推广,在直角三角形中，一个锐角的正切值等于其对边长度与邻边长度的比值，用数学符号表示为：

[ \tan \theta = \frac{\text{对边}}{\text{邻边}} = \frac{\sin \theta}{\cos \theta} ]

在单位圆中,角θ的正切值等于该角终边与单位圆交点的纵坐标与横坐标的比值，当θ=45°时，tan45°=1。

正切函数的周期为180°，且是奇函数，即tan(-θ) = -tanθ，需要注意的是，当θ=90°时，cosθ=0，因此tanθ无定义。

三者的相互关系

正弦、余弦、正切之间存在密切的联系。

• (\tan \theta = \frac{\sin \theta}{\cos \theta})
• (\sin^2 \theta + \cos^2 \theta = 1)（毕达哥拉斯恒等式）

这些关系在三角恒等式的推导和计算中非常重要。

实际应用

三角函数在现实生活中有广泛的应用。

1. 物理学中：描述简谐运动（如弹簧振子、声波）时，正弦和余弦函数常被用来表示波形。
2. 工程学中：在电路分析、信号处理等领域，三角函数用于分析交流电的电压和电流。
3. 几何学中：通过三角函数可以计算三角形的边长和角度，解决实际测量问题。