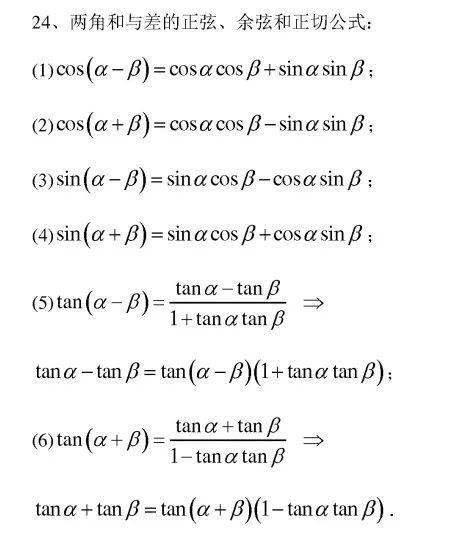三角函数公式大全表格倍角公式：三角函数公式大全，基础、倍角与常用恒等式

三角函数是数学中一个重要的基础部分,广泛应用于几何、物理、工程、计算机科学等领域，掌握三角函数的各类公式对于解决相关问题至关重要，本文将为您梳理三角函数的核心公式，重点介绍倍角公式，并以表格形式（文字描述版）呈现，方便查阅和记忆。

基本概念与定义

在介绍公式前,我们先回顾一下基本定义：

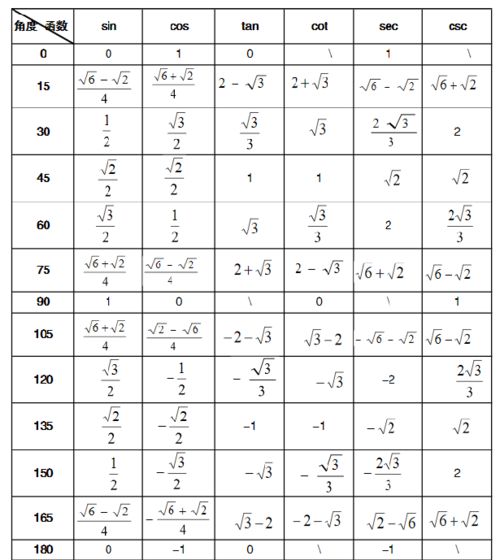
• 角度制： 0°, 30°, 45°, 60°, 90°, ...
• 弧度制： 0, π/6, π/4, π/3, π/2, π, ...
• 直角三角形定义：
  • sinθ = 对边 / 斜边
  • cosθ = 邻边 / 斜边
  • tanθ = 对边 / 邻边
• 单位圆定义： 利用单位圆（半径为1的圆）上的点坐标来定义。

基本函数关系与恒等式

1. 平方关系：

   • sin²θ + cos²θ = 1
   • 1 + tan²θ = sec²θ (secθ = 1/cosθ)
   • 1 + cot²θ = csc²θ (cscθ = 1/sinθ)

2. 倒数关系：

   • sinθ * cscθ = 1
   • cosθ * secθ = 1
   • tanθ * cotθ = 1

3. 商数关系：

   • tanθ = sinθ / cosθ
   • cotθ = cosθ / sinθ

角度关系公式（诱导公式）

这些公式描述了不同角度（如 θ, -θ, π±θ, 2π±θ 等）的三角函数值与 θ 的三角函数值之间的关系。

• θ 的奇偶性：
  • sin(-θ) = -sinθ
  • cos(-θ) = cosθ
  • tan(-θ) = -tanθ
• θ + π/2：
  • sin(θ + π/2) = cosθ
  • cos(θ + π/2) = -sinθ
  • tan(θ + π/2) = -cotθ
• • sin(θ + π) = -sinθ
  • cos(θ + π) = -cosθ
  • tan(θ + π) = tanθ
• θ + 3π/2：
  • sin(θ + 3π/2) = -cosθ
  • cos(θ + 3π/2) = sinθ
  • tan(θ + 3π/2) = -cotθ
• θ + 2kπ (k为整数)： 函数值不变。
• θ + kπ (k为整数)： 正弦、余弦函数值变号（k为奇数），不变（k为偶数）；正切、余切函数值不变。

和差角公式

这些公式用于计算两个角的和或差的正弦、余弦、正切值。

• 正弦加法公式：
  • sin(A + B) = sinA cosB + cosA sinB
  • sin(A - B) = sinA cosB - cosA sinB
• 余弦加法公式：
  • cos(A + B) = cosA cosB - sinA sinB
  • cos(A - B) = cosA cosB + sinA sinB
• 正切加法公式：
  • tan(A + B) = (tanA + tanB) / (1 - tanA tanB) (当 1 - tanA tanB ≠ 0)
  • tan(A - B) = (tanA - tanB) / (1 + tanA tanB) (当 1 + tanA tanB ≠ 0)

倍角公式

倍角公式是和差角公式的特例,将其中一个角设为 θ，另一个角也设为 θ，从而得到倍角（如 2θ, 3θ 等）的三角函数表达式，这是本节的重点。

• 二倍角公式 (2θ)：

  • sin(2θ) = 2 sinθ cosθ
  • cos(2θ) = cos²θ - sin²θ = 2cos²θ - 1 = 1 - 2sin²θ
  • tan(2θ) = 2tanθ / (1 - tan²θ) (当 1 - tan²θ ≠ 0)

• 三倍角公式 (3θ)：

  • sin(3θ) = 3sinθ - 4sin³θ
  • cos(3θ) = 4cos³θ - 3cosθ
  • tan(3θ) = (3tanθ - tan³θ) / (1 - 3tan²θ) (当分母不为零)

• 四倍角公式 (4θ)： 可以通过二倍角公式嵌套得到，cos(4θ) = 2cos²(2θ) - 1 = 2(2cos²θ - 1)² - 1 等。

• 半角公式 (θ/2)： 用于计算半角的三角函数值。

  • sin(θ/2) = ±√((1 - cosθ) / 2)
  • cos(θ/2) = ±√((1 + cosθ) / 2)
  • tan(θ/2) = ±√((1 - cosθ) / (1 + cosθ)) 或 sinθ / (1 + cosθ) 或 (1 - cosθ) / sinθ (符号取决于 θ/2 所在的象限)

和差化积公式

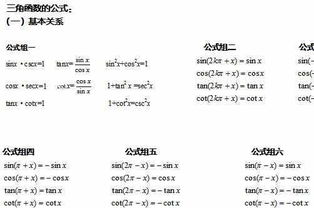
将两个角的和或差的三角函数转化为它们的积的形式。

• 正弦加法/减法化积：
  • sinA + sinB = 2 sin((A+B)/2) cos((A-B)/2)
  • sinA - sinB = 2 cos((A+B)/2) sin((A-B)/2)
• 余弦加法/减法化积：
  • cosA + cosB = 2 cos((A+B)/2) cos((A-B)/2)
  • cosA - cosB = -2 sin((A+B)/2) sin((A-B)/2)
• 正切加法/减法化积： 较为复杂，通常在特定情况下使用。

积化和差公式

将两个角的三角函数的乘积转化为和或差的形式。

• sinA cosB = (1/2) [sin(A+B) + sin(A-B)]
• cosA sinB = (1/2) [sin(A+B) - sin(A-B)]
• cosA cosB = (1/2) [cos(A+B) + cos(A-B)]
• sinA sinB = (1/2) [cos(A-B) - cos(A+B)]

是三角函数的主要公式体系,掌握这些公式需要理解其推导过程，并通过大量的练习来加深记忆和灵活运用，特别是倍角公式（如二倍角、三倍角），在求值、化简、证明恒等式以及解三角方程中应用非常广泛。

（可选：此处可以插入一个表格，列出主要倍角公式，）

| 倍数 | 角度 | 正弦 sin(nθ) | 余弦 cos(nθ) | 正切 tan(nθ) (条件) | | ：--- | :--- | :----------- | :----------- | :------------------ | | 1 | θ | sinθ | cosθ | tanθ | | 2 | 2θ | 2sinθcosθ | cos²θ-sin²θ | 2tanθ/(1-tan²θ) | | 3 | 3θ | 3sinθ-4sin³θ | 4cos³θ-3cosθ | (3tanθ-tan³θ)/(1-3tan²θ) | | ... | ... | ... | ... | ... |

希望这篇文章能帮助您系统地复习和掌握三角函数公式！如果您需要更详细的推导过程或具体应用示例，请随时告知。