反比例函数十大经典题型：反比例函数十大经典题型及解题策略

反比例函数是初中数学中的重要知识点，也是中考数学的必考内容之一，掌握反比例函数的图像、性质及其应用，对于学生来说至关重要，本文将围绕反比例函数的十大经典题型展开讲解，帮助学生在解题过程中掌握方法、提升能力。

反比例函数的基本概念

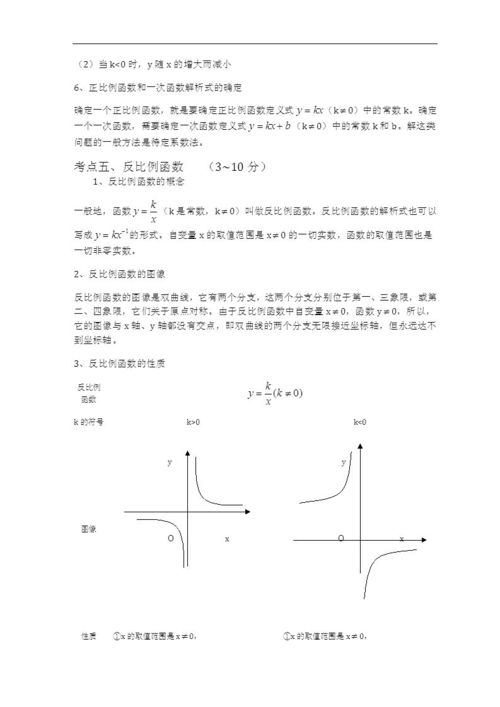
反比例函数是指函数形式为 ( y = \frac{k}{x} )（( k ) 是常数且 ( k \neq 0 )）的函数，其图像为双曲线,具有以下特点：

• 当 ( k > 0 ) 时，图像位于一、三象限；
• 当 ( k < 0 ) 时，图像位于二、四象限；
• 图像关于原点中心对称。

十大经典题型解析

图像识别与性质判断

例题：
已知反比例函数 ( y = \frac{6}{x} )，则下列说法正确的是（ ）
A. 图像经过点（-2，-3）
B. 当 ( x > 0 ) 时，y 随 x 增大而减小
C. 图像在第二、四象限
D. 函数值 y 随 x 增大而增大

解析：

• A 选项：将 ( x = -2 ) 代入得 ( y = \frac{6}{-2} = -3 )，点（-2，-3）在图像上，正确。
• B 选项：当 ( x > 0 ) 时，k=6>0，y 随 x 增大而减小，正确。
• C 选项：k=6>0，图像应在第一、三象限，错误。
• D 选项：反比例函数不具有单调性，错误。

答案： B

求反比例函数的表达式

例题：
已知点（2，3）在反比例函数 ( y = \frac{k}{x} ) 的图像上，求 k 的值，并写出函数表达式。

解析：
将点（2，3）代入 ( y = \frac{k}{x} )：
( 3 = \frac{k}{2} )
解得 ( k = 6 )
因此函数表达式为 ( y = \frac{6}{x} )。

图像与坐标轴的交点

例题：
反比例函数 ( y = \frac{-4}{x} ) 的图像与坐标轴的交点个数是（ ）
A. 0 个
B. 1 个
C. 2 个
D. 3 个

解析：
反比例函数的图像不与坐标轴相交，因为当 ( x=0 ) 时，y 无定义；当 ( y=0 ) 时，x 无定义，因此交点个数为 0。

答案： A

图像的对称性

例题：
反比例函数 ( y = \frac{k}{x} ) 的图像关于原点对称，若点（1，2）在其图像上，则点（-1，-2）是否也在其图像上？

解析：
由于图像关于原点对称，若点（1，2）在图像上，则点（-1，-2）也一定在图像上。
验证：将（1，2）代入得 ( k=2 )，函数为 ( y=\frac{2}{x} )，将（-1，-2）代入得 ( y=\frac{2}{-1}=-2 )，符合。

反比例函数与一次函数的交点

例题：
求反比例函数 ( y = \frac{6}{x} ) 与一次函数 ( y = x + 2 ) 的交点坐标。

解析：
联立方程：
( \frac{6}{x} = x + 2 )
两边乘以 x（x≠0）：
6 = x² + 2x
x² + 2x - 6 = 0
解得 ( x = -1 \pm \sqrt{7} )
代入得 y 值，交点为 ( (-1 + \sqrt{7}, 3 + \sqrt{7}) ) 和 ( (-1 - \sqrt{7}, 3 - \sqrt{7}) )。

反比例函数的实际应用

例题：
某工程队计划用若干天完成一项工程，已知每天完成的工作量与所需天数成反比，若每天完成 100 个单位，则需 12 天完成，求：
（1）总工作量是多少？
（2）若每天完成 150 个单位，则需多少天完成？

解析：
设总工作量为 W，每天完成量为 y，所需天数为 x，则 ( y = \frac{W}{x} )。
（1）由题意，y=100，x=12，得 ( 100 = \frac{W}{12} )，解得 W=1200。
（2）y=150，( 150 = \frac{1200}{x} )，解得 x=8 天。

反比例函数的参数变化

例题：
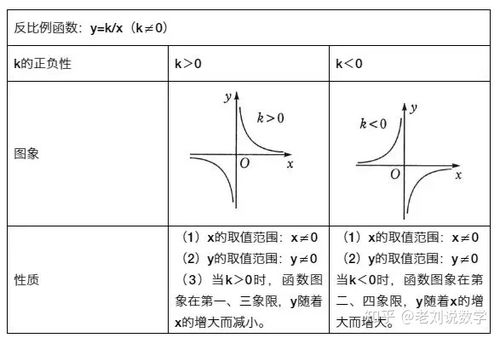
当 k 从正数变为负数时，反比例函数 ( y = \frac{k}{x} ) 的图像如何变化？

解析：
当 k>0 时，图像在第一、三象限；当 k<0 时，图像在第二、四象限，k 的符号变化会导致图像位于不同的象限。

反比例函数与不等式结合

例题：
若 ( y = \frac{6}{x} > 2 )，求 x 的取值范围。

解析：
( \frac{6}{x} > 2 )
分情况讨论：

• 当 x>0 时，6 > 2x，解得 x<3
• 当 x<0 时，不等式两边乘以负数，方向改变，6 < 2x，解得 x>3（但 x<0，无解）
  x 的取值范围为 0 < x < 3。

反比例函数与几何图形结合

例题：
在直角坐标系中，点 A（1，a）和 B（b，2）均在反比例函数 ( y = \frac{4}{x} ) 的图像上，求 a 和 b 的值。

解析：
将 A（1，a）代入：a = \frac{4}{1} = 4
将 B（b，2）代入：2 = \frac{4}{b}，解得 b=2
a=4，b=2。

反比例函数的综合题

例题：
已知反比例函数 ( y = \frac{k}{x} ) 与一次函数 ( y = mx + n ) 相交于点（1，k）和（-1，-k），求 k、m、n 的值。

解析：
（1）点（1，k）在反比例函数上：k = \frac{k}{1}，恒成立。
（2）点（-1，-k）在反比例函数上：-k = \frac{k}{-1}，恒成立。
（3）点（1，k）在一次函数上：k = m + n
（4）点（-1，-k）在一次函数上：-k = -m + n
解方程组：
k = m + n
-k = -m + n
两式相加：0 = 2n，解得 n=0
代入得 k = m
k、m、n 的值满足 n=0，k=m，k 任意（但 k≠0）。

反比例函数是中考数学中的重要考点，题型多样，涉及图像、性质、表达式、应用等多个方面,学生在解题时应注重以下几点：

1. 数形结合：通过图像理解函数性质；
2. 分类讨论：在解不等式或参数变化时注意分情况讨论；
3. 实际应用：理解反比例函数在生活中的应用,如工作量与时间的关系；
4. 综合题训练：提高逻辑推理和方程求解能力。

通过不断练习和总结，学生可以更好地掌握反比例函数的相关知识,提高解题能力。