绝对值函数怎么画：绝对值函数怎么画？手把手教你画出完美图像

什么是绝对值函数？

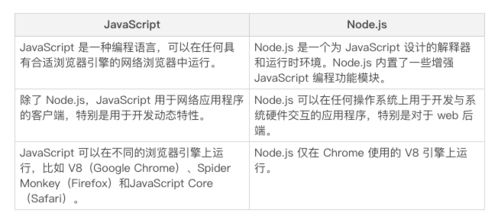
绝对值函数是指函数中的自变量被绝对值符号所包围，

[ f(x) = |x| ]

其定义为：

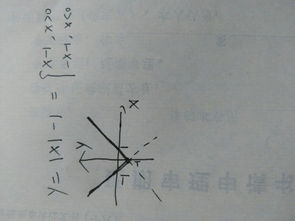
[ |x| = \begin{cases} x & \text{if } x \geq 0 \ -x & \text{if } x < 0 \end{cases} \end{aligned} ]

绝对值函数的本质是表示数轴上某点到原点的距离，因此其图像总是非负的，且关于 y 轴对称。

画绝对值函数的步骤

绘制绝对值函数的图像可以分为以下几个步骤：

确定关键点

绝对值函数的图像通常有一个“V”字形转折点，称为顶点,顶点的位置取决于函数内部的表达式。

对于 ( f(x) = |x - a| )，顶点位于 ((a, 0))。

分析函数的分段线性性质

绝对值函数在不同区间内是线性的,因此可以通过分段讨论来绘制图像。

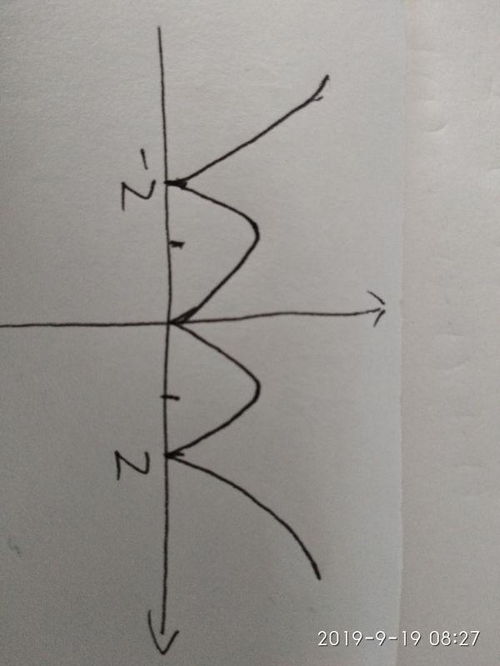
对于 ( f(x) = |x - 2| )：

• 当 ( x \geq 2 ) 时，( f(x) = x - 2 )
• 当 ( x < 2 ) 时，( f(x) = -(x - 2) = -x + 2 )

连接图像

根据分段线性表达式，分别画出每一段的直线,然后在转折点处平滑连接。

绘制示例：( y = |x - 2| )

确定顶点

顶点为 ((2, 0))，因为当 ( x = 2 ) 时，( y = 0 )。

分段绘制

• 当 ( x \geq 2 ) 时，( y = x - 2 )，是一条斜率为 1、过点 ((2, 0)) 的直线。
• 当 ( x < 2 ) 时，( y = -x + 2 )，是一条斜率为 -1、过点 ((2, 0)) 的直线。

绘制图像

1. 在坐标系中标出顶点 ((2, 0))。
2. 向右延伸：从 ((2, 0)) 开始，沿斜率 1 向上画直线。
3. 向左延伸：从 ((2, 0)) 开始，沿斜率 -1 向上画直线。

最终图像为一个顶点在 ((2, 0)) 的“V”字形图像。

实用技巧

1. 注意顶点位置：顶点是图像的关键点，决定了“V”字形的开口方向。
2. 考虑定义域：如果函数定义域有限,图像可能会被截断。
3. 利用对称性：绝对值函数通常具有对称性,可以利用对称点简化绘图。
4. 多练习：通过绘制不同形式的绝对值函数（如 ( y = |x| + k )、( y = |x - a| + b ) 等）,加深理解。

绝对值函数的图像虽然简单，但却是理解更复杂函数的基础，通过掌握其分段线性性质和顶点位置，你可以轻松绘制出准确的图像，多加练习，你会发现画图不仅是一种技能,更是一种直观理解函数本质的工具。