三角函数公式大全表图：三角函数公式大全表图，从基础到进阶的全面解析

三角函数的基本定义

三角函数是数学中描述角度与边长关系的重要函数，主要包括正弦（sin）、余弦（cos）、正切（tan）、余切（cot）、正割（sec）和余割（csc）,其定义如下：

1. 直角三角形定义：

   • sinθ = 对边 / 斜边
   • cosθ = 邻边 / 斜边
   • tanθ = 对边 / 邻边

2. 单位圆定义：

   • sinθ = y 坐标
   • cosθ = x 坐标
   • tanθ = y/x

诱导公式

诱导公式用于将任意角度的三角函数转化为锐角三角函数,主要包括以下几类：

1. 角度加减2π：

   • sin(θ + 2kπ) = sinθ
   • cos(θ + 2kπ) = cosθ
   • tan(θ + 2kπ) = tanθ

2. 角度加减π：

   • sin(θ + π) = -sinθ
   • cos(θ + π) = -cosθ
   • tan(θ + π) = tanθ

3. 角度加减π/2：

   • sin(θ + π/2) = cosθ
   • cos(θ + π/2) = -sinθ
   • tan(θ + π/2) = -cotθ

和差角公式

和差角公式用于计算两个角的和或差的三角函数值：

1. 正弦和角公式：

   • sin(A + B) = sinA cosB + cosA sinB
   • sin(A - B) = sinA cosB - cosA sinB

2. 余弦和角公式：

   • cos(A + B) = cosA cosB - sinA sinB
   • cos(A - B) = cosA cosB + sinA sinB

3. 正切和角公式：

   • tan(A + B) = (tanA + tanB) / (1 - tanA tanB)
   • tan(A - B) = (tanA - tanB) / (1 + tanA tanB)

倍角公式

倍角公式用于计算两倍角的三角函数值：

1. 正弦倍角公式：

   sin(2θ) = 2 sinθ cosθ

2. 余弦倍角公式：

   cos(2θ) = cos²θ - sin²θ = 2cos²θ - 1 = 1 - 2sin²θ

3. 正切倍角公式：

   tan(2θ) = 2 tanθ / (1 - tan²θ)

半角公式

半角公式用于计算半角的三角函数值：

1. 正弦半角公式：

   sin(θ/2) = ±√((1 - cosθ) / 2)

   

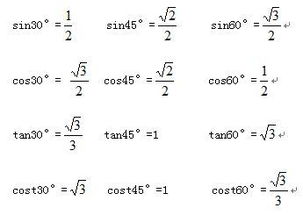
2. 余弦半角公式：

   cos(θ/2) = ±√((1 + cosθ) / 2)

3. 正切半角公式：

   tan(θ/2) = ±√((1 - cosθ) / (1 + cosθ))

万能公式

万能公式通过正切函数的一半角关系,将三角函数转化为正切函数的形式：

1. 正弦万能公式：

   sinθ = 2 tan(θ/2) / (1 + tan²(θ/2))

2. 余弦万能公式：

   cosθ = (1 - tan²(θ/2)) / (1 + tan²(θ/2))

   

3. 正切万能公式：

   tanθ = 2 tan(θ/2) / (1 - tan²(θ/2))

积化和差与和差化积公式

1. 积化和差公式：

   • sinA cosB = [sin(A+B) + sin(A-B)] / 2
   • cosA sinB = [sin(A+B) - sin(A-B)] / 2
   • cosA cosB = [cos(A+B) + cos(A-B)] / 2
   • sinA sinB = [cos(A-B) - cos(A+B)] / 2

2. 和差化积公式：

   • sinA + sinB = 2 sin((A+B)/2) cos((A-B)/2)
   • sinA - sinB = 2 cos((A+B)/2) sin((A-B)/2)
   • cosA + cosB = 2 cos((A+B)/2) cos((A-B)/2)
   • cosA - cosB = -2 sin((A+B)/2) sin((A-B)/2)

其他常用公式

1. 三角恒等式：

   • sin²θ + cos²θ = 1
   • 1 + tan²θ = sec²θ
   • 1 + cot²θ = csc²θ

2. 三角函数的周期性：

   • sinθ 和 cosθ 的周期为 2π
   • tanθ 和 cotθ 的周期为 π

记忆技巧

1. 口诀记忆：

   “奇变偶不变，符号看象限”——用于记忆诱导公式。

2. 图形辅助：

   通过单位圆和三角函数图像,直观理解公式的几何意义。

三角函数公式是数学学习中的重要工具，掌握这些公式不仅能提高解题效率，还能加深对三角函数本质的理解，建议通过多练习、多总结，逐步将这些公式内化为自己的知识储备，如果需要更直观的图表形式,可以参考数学教材或使用数学软件绘制函数图像。