函数与反函数的关系公式：函数与反函数的关系公式，探秘数学中的逆向映射

函数与反函数的定义

函数是一种映射关系,即对于定义域内的每一个输入值，都有唯一的输出值，通常表示为 ( f: A \to B )，( A ) 是定义域，( B ) 是值域。

反函数则是函数的逆映射,只有当原函数是一一映射（即单射且满射）时，才存在反函数，反函数通常表示为 ( f^{-1} )，它将原函数的输出值映射回输入值。

函数与反函数的关系公式

函数与反函数之间最核心的关系是：

[ f(f^{-1}(x)) = x \quad \text{和} \quad f^{-1}(f(x)) = x ]

这两个公式表明,函数与反函数的复合结果是恒等函数，即它们相互“抵消”。

复合函数的恒等性

( y = f(x) )，则 ( x = f^{-1}(y) )，将 ( y ) 代入反函数中，得到：

[ f^{-1}(f(x)) = x ]

同样,将 ( x ) 代入函数中，再代入反函数，得到：

[ f(f^{-1}(x)) = x ]

图像的对称性

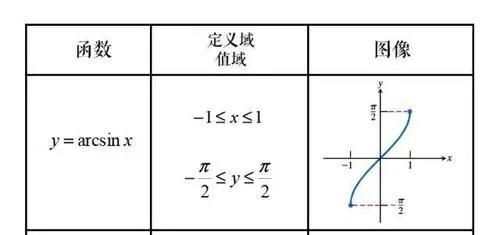
函数与反函数的图像关于直线 ( y = x ) 对称，这一性质在图形化表示中尤为直观。

常见函数的反函数公式

线性函数

对于线性函数 ( y = mx + b )（( m \neq 0 )），其反函数为：

[ y = \frac{x - b}{m} ]

指数函数与对数函数

指数函数 ( y = a^x )（( a > 0 ) 且 ( a \neq 1 )）的反函数是对数函数：

[ y = \log_a x ]

二次函数

二次函数 ( y = ax^2 + bx + c )（( a \neq 0 )）的反函数需要限制定义域，使其成为一一映射，定义域为 ( x \geq 0 ) 时，反函数为：

[ x = \sqrt{\frac{-b + \sqrt{b^2 - 4ac}}{2a}} ]

应用与意义

函数与反函数的关系公式在数学、物理、工程等领域有广泛应用。

• 在解方程时,反函数可以帮助我们求解未知数。
• 在数据建模中,反函数用于处理逆向关系。
• 在计算机科学中,反函数用于密码学和编码解码。

函数与反函数的关系公式是数学中的重要工具,它们通过复合恒等性和图像对称性紧密联系，理解这些关系不仅有助于掌握数学理论，还能在实际问题中灵活应用，希望本文能帮助你更好地理解函数与反函数之间的关系，为你的学习和研究提供支持。