初等函数的性质：初等函数的性质与分类

来源：网络作者：日期：2025-11-06 03:45:45

初等函数是数学中一类基本的函数，它们在微积分、高等数学以及各种应用学科中占据核心地位，初等函数不仅包括常数函数、幂函数、指数函数、对数函数、三角函数和双曲函数等，还涵盖了这些函数的有限次组合，如加、减、乘、除、乘方、开方等运算，初等函数的性质是理解更复杂函数的基础,因此掌握其基本性质对于数学学习至关重要。

初等函数的定义

初等函数是指由常数、变量以及基本运算符号（如加、减、乘、除、乘方、开方）和基本函数（如幂函数、指数函数、对数函数、三角函数等）通过有限次组合而成的函数,初等函数可以分为代数函数和超越函数两大类。

初等函数的分类及其性质

常数函数

常数函数是指函数值恒为常数的函数，形式为 ( f(x) = c )，( c ) 为常数。

定义域：全体实数 ( \mathbb{R} )。
值域：单点集 ( {c} )。
图像：一条水平直线。
性质：常数函数是偶函数，且在整个定义域上单调递增或递减（取决于常数的变化，但通常视为常数）。

幂函数

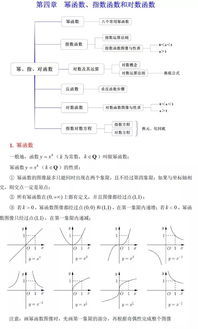
幂函数是指形式为 ( f(x) = x^a ) 的函数，( a ) 为常数。

初等函数的性质：初等函数的性质与分类

定义域：取决于指数 ( a )，若 ( a ) 为整数，则定义域为 ( \mathbb{R} )；若 ( a ) 为分数,则定义域需根据分母确定。
值域：取决于 ( a ) 的值，可能为 ( [0, +\infty) ) 或 ( \mathbb{R} ) 等。
图像：根据指数的不同，图像可能为过原点的直线、抛物线、双曲线等。
性质：幂函数具有单调性，且在 ( x > 0 ) 时具有奇偶性（若 ( a ) 为整数）。

指数函数

指数函数是指形式为 ( f(x) = a^x ) 的函数，( a > 0 ) 且 ( a \neq 1 )。

定义域：全体实数 ( \mathbb{R} )。
值域：若 ( a > 1 )，则值域为 ( (0, +\infty) )；若 ( 0 < a < 1 )，则值域同样为 ( (0, +\infty) )。
图像：过点 ( (0, 1) )，且当 ( a > 1 ) 时单调递增，当 ( 0 < a < 1 ) 时单调递减。
性质：指数函数具有周期性（无周期），且具有对称性（如 ( a^x ) 与 ( a^{-x} ) 互为倒数）。

对数函数

对数函数是指形式为 ( f(x) = \log_a x ) 的函数，( a > 0 ) 且 ( a \neq 1 )。

定义域：( (0, +\infty) )。
值域：全体实数 ( \mathbb{R} )。
图像：过点 ( (1, 0) )，且当 ( a > 1 ) 时单调递增，当 ( 0 < a < 1 ) 时单调递减。
性质：对数函数是指数函数的逆运算，具有单调性、对称性（如 ( \log_a (xy) = \log_a x + \log_a y )）。

三角函数

三角函数包括正弦、余弦、正切等基本函数，形式如 ( f(x) = \sin x )、( f(x) = \cos x )、( f(x) = \tan x ) 等。

初等函数的性质：初等函数的性质与分类

定义域：取决于具体函数，如正弦和余弦的定义域为 ( \mathbb{R} )，正切函数的定义域为 ( x \neq \frac{\pi}{2} + k\pi )（( k ) 为整数）。
值域：正弦和余弦的值域为 ( [-1, 1] )，正切函数的值域为 ( \mathbb{R} )。
图像：周期性、波浪形图像。
性质：三角函数具有周期性、奇偶性（如正弦为奇函数，余弦为偶函数）,且具有对称性。