gamma函数怎么算：Gamma函数的计算方法与应用

Gamma函数（Γ函数）是数学中一个重要的特殊函数，由丹尼尔·伯努利（Daniel Bernoulli）在1729年首次引入，后由路易斯·卡塔兰（Louis Catalan）和卡尔·弗里德里希·高斯（Carl Friedrich Gauss）等人进一步发展，Gamma函数在数学、物理、统计学和工程学等领域有广泛应用，尤其在概率论和统计分布中扮演着关键角色，本文将详细介绍Gamma函数的定义、性质以及几种常用的计算方法。

Gamma函数的定义

Gamma函数的定义如下： [ \Gamma(z) = \int_0^\infty x^{z-1} e^{-x} dx ] ( z ) 是一个复数，且 ( \text{Re}(z) > 0 )，这个积分定义了Gamma函数,它将函数扩展到非整数参数。

Gamma函数的性质

1. 函数方程：Gamma函数满足以下函数方程： [ \Gamma(z+1) = z \Gamma(z) ] 这个性质使得Gamma函数在整数点上的值与阶乘相关，即 ( \Gamma(n) = (n-1)! ) 对于正整数 ( n )。

2. 解析延拓：Gamma函数可以通过解析延拓定义到整个复平面（除了非负整数点）,其中它在负整数点有极点。

3. 对称性：Gamma函数与反射公式相关： [ \Gamma(z) \Gamma(1-z) = \frac{\pi}{\sin(\pi z)} ] 这个性质在复变函数中尤为重要。

Gamma函数的计算方法

Gamma函数的计算可以通过多种方法实现,以下是几种常见的方法：

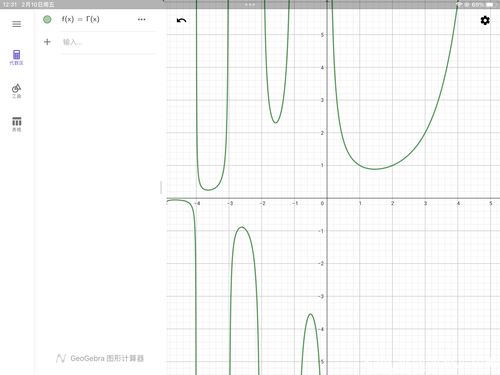
1. 数值积分法： Gamma函数的定义式是一个积分，因此可以通过数值积分方法（如梯形法、辛普森法或高斯积分）来近似计算，对于 ( z = 0.5 )，可以计算： [ \Gamma(0.5) = \int_0^\infty x^{-0.5} e^{-x} dx ] 通过数值积分，可以得到 ( \Gamma(0.5) = \sqrt{\pi} \approx 1.77245 )。

2. 级数展开法： 对于某些参数，Gamma函数可以通过级数展开来计算，对于正实数 ( z )，可以使用以下级数： [ \Gamma(z) = \sum_{n=0}^\infty \frac{(-1)^n}{n!} \gamma(z+n) ] ( \gamma ) 是Euler-Mascheroni常数。

3. 递推关系法： 利用Gamma函数的函数方程 ( \Gamma(z+1) = z \Gamma(z) )，可以将Gamma函数的计算转化为已知值的计算，计算 ( \Gamma(5) )： [ \Gamma(5) = 4 \Gamma(4) = 4 \times 3 \Gamma(3) = 4 \times 3 \times 2 \Gamma(2) = 4 \times 3 \times 2 \times 1 \Gamma(1) = 24 \times 1 = 24 ] 因为 ( \Gamma(1) = 1 )。

   

4. 查表法： 对于常见的Gamma函数值,可以使用预先计算好的表格。

   • ( \Gamma(1) = 1 )
   • ( \Gamma(2) = 1! = 1 )
   • ( \Gamma(3) = 2! = 2 )
   • ( \Gamma(0.5) = \sqrt{\pi} \approx 1.77245 )

Gamma函数的应用

1. 概率论与统计学： Gamma函数在概率论中用于定义Gamma分布、卡方分布和t分布等，Gamma分布的概率密度函数为： [ f(x; k, \theta) = \frac{x^{k-1} e^{-x/\theta}}{\theta^k \Gamma(k)} ] ( k ) 是形状参数，( \theta ) 是尺度参数。

2. 复变函数： Gamma函数在复变函数理论中用于定义黎曼ζ函数和调和ζ函数等。

3. 物理学： 在量子力学和统计力学中,Gamma函数用于描述粒子的能级和分布。

Gamma函数是一个强大而灵活的数学工具，其计算方法多样，应用广泛，掌握Gamma函数的计算方法不仅有助于解决数学问题，还能在多个学科中发挥重要作用，通过本文的介绍，希望读者能够对Gamma函数有一个全面的理解,并能够在实际问题中灵活运用。