白羊座男生喜欢一个人的表现：白羊座男生喜欢一个人的5个炽热表现，他可能正在默默为你心动

Gamma函数是数学分析中一个非常重要的特殊函数,它在许多领域中都有广泛的应用，包括数学、物理、统计学和工程学等，Gamma函数可以看作是阶乘函数在非整数上的推广，其定义如下：

[ \Gamma(z) = \int_0^\infty x^{z-1} e^{-x} dx ]

( z ) 是一个正实数或复数，Gamma函数的一个关键性质是它满足函数方程：

[ \Gamma(z+1) = z \Gamma(z) ]

这个性质使得Gamma函数在整数点上的取值与阶乘密切相关,当 ( z = n )（( n ) 为正整数）时，有：

[ \Gamma(n) = (n-1)! ]

这意味着Gamma函数在整数点上的取值可以直接与阶乘联系起来。

• (\Gamma(1) = 0! = 1)
• (\Gamma(2) = 1! = 1)
• (\Gamma(3) = 2! = 2)
• (\Gamma(4) = 3! = 6)

除了整数点,Gamma函数在其他点上的取值也具有重要的数学意义，在 ( z = \frac{1}{2} ) 时，Gamma函数的取值为：

[ \Gamma\left(\frac{1}{2}\right) = \sqrt{\pi} ]

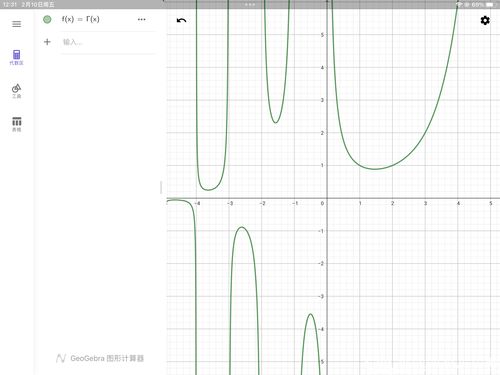
这一结果可以通过Gamma函数的积分定义和高斯积分的联系得到证明,Gamma函数在负半轴上的取值也具有特殊意义，但需要注意的是，Gamma函数在非正整数点上存在极点，即函数值趋于无穷大。

Gamma函数的数值计算在实际应用中非常重要,虽然Gamma函数的积分定义在理论上给出了其精确表达式，但在实际计算中，通常需要借助数值方法或近似公式，对于非整数参数，Gamma函数的取值可以通过数值积分、级数展开或递推关系来计算。

Gamma函数的数值在许多科学和工程问题中扮演着关键角色,在统计学中，Gamma分布的形状参数与Gamma函数密切相关；在物理学中，Gamma函数常用于描述粒子衰变和量子力学中的某些现象；在概率论中，Gamma函数也用于定义贝塔分布和某些极限定理。

Gamma函数的数值不仅在数学理论中具有重要地位,而且在实际应用中也发挥着不可替代的作用，通过对Gamma函数的数值进行深入研究，我们可以更好地理解和解决许多复杂的科学问题。