对数函数的导数推导过程：对数函数的导数推导过程

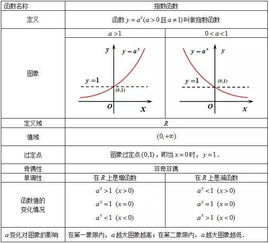
对数函数的定义

对数函数定义为：若 ( a^b = c )，则 ( b = \log_a c )，( a > 0 ) 且 ( a \neq 1 )，( c > 0 )，自然对数函数 ( \ln x ) 是以自然常数 ( e \approx 2.71828 ) 为底的对数函数。

对数函数的导数推导

设函数 ( f(x) = \ln x )，求其导数 ( f'(x) )。

定义导数

导数的定义为：

[ f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} ]

代入 ( f(x) = \ln x )：

[ f'(x) = \lim_{\Delta x \to 0} \frac{\ln(x + \Delta x) - \ln x}{\Delta x} ]

利用对数性质简化

根据对数性质 ( \ln a - \ln b = \ln \frac{a}{b} ),可得：

[ f'(x) = \lim{\Delta x \to 0} \frac{\ln \left( \frac{x + \Delta x}{x} \right)}{\Delta x} = \lim{\Delta x \to 0} \frac{\ln \left( 1 + \frac{\Delta x}{x} \right)}{\Delta x} ]

变量替换

令 ( t = \frac{\Delta x}{x} )，则当 ( \Delta x \to 0 ) 时，( t \to 0 )，且 ( \Delta x = t \cdot x ),代入得：

[ f'(x) = \lim{t \to 0} \frac{\ln (1 + t)}{t \cdot x} = \frac{1}{x} \lim{t \to 0} \frac{\ln (1 + t)}{t} ]

求极限

已知极限 ( \lim_{t \to 0} \frac{\ln (1 + t)}{t} = 1 )，

[ f'(x) = \frac{1}{x} \cdot 1 = \frac{1}{x} ]

一般对数函数的导数

对于一般对数函数 ( \log_a x ),其导数可通过换底公式推导：

[ \log_a x = \frac{\ln x}{\ln a} ]

[ \frac{d}{dx} (\log_a x) = \frac{d}{dx} \left( \frac{\ln x}{\ln a} \right) = \frac{1}{\ln a} \cdot \frac{d}{dx} (\ln x) = \frac{1}{\ln a} \cdot \frac{1}{x} = \frac{1}{x \ln a} ]

通过对数函数的定义和导数的极限定义,我们推导出：

• 自然对数函数的导数：( \frac{d}{dx} (\ln x) = \frac{1}{x} )
• 一般对数函数的导数：( \frac{d}{dx} (\log_a x) = \frac{1}{x \ln a} )

这一推导过程不仅展示了对数函数的导数公式，也为后续学习复合函数、积分等微积分内容奠定了基础。