幂函数的运算法则：幂函数的运算法则，掌握数学运算的核心技巧

幂函数的定义

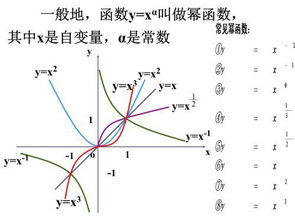
幂函数是指形如 ( f(x) = x^n ) 的函数，( x ) 是自变量，( n ) 是常数，称为指数，幂函数的定义域和值域取决于指数 ( n ) 的值，

• 当 ( n ) 为整数时，定义域为全体实数；
• 当 ( n ) 为分数时，定义域可能受到限制。

幂函数的基本运算法则

幂函数的运算主要遵循以下几条法则,这些法则在指数运算中具有普遍适用性。

同底数幂的乘法法则

当两个幂函数具有相同的底数时,其乘法规则为：

[ a^m \cdot a^n = a^{m+n} ]

示例：

[ 2^3 \cdot 2^4 = 2^{3+4} = 2^7 = 128 ]

同底数幂的除法法则

当两个幂函数具有相同的底数时,其除法规则为：

[ \frac{a^m}{a^n} = a^{m-n} \quad (a \neq 0) ]

示例：

[ \frac{3^5}{3^2} = 3^{5-2} = 3^3 = 27 ]

幂的乘方法则

当一个幂函数被另一个幂所乘时,其运算法则为：

[ (a^m)^n = a^{m \cdot n} ]

示例：

[ (4^2)^3 = 4^{2 \cdot 3} = 4^6 = 4096 ]

零指数法则

任何非零数的零次幂等于 1：

[ a^0 = 1 \quad (a \neq 0) ]

示例：

[ 5^0 = 1, \quad (-3)^0 = 1 ]

负指数法则

负指数幂可以转化为倒数形式：

[ a^{-n} = \frac{1}{a^n} \quad (a \neq 0) ]

示例：

[ 2^{-3} = \frac{1}{2^3} = \frac{1}{8} ]

不同底数幂的运算

当底数不同时,幂函数的运算需要借助其他法则，如交换律、结合律和分配律，但需注意以下特殊情况：

• 底数为负数时：负底数的幂函数结果可能为负数或复数，需谨慎处理。
• 底数为零时：零的负指数幂无定义，零的正指数幂为零。

分数指数幂的运算

分数指数幂可以表示为根式形式,其运算法则与整数指数幂类似：

[ a^{\frac{m}{n}} = \sqrt[n]{a^m} \quad \text{或} \quad (\sqrt[n]{a})^m ]

示例：

[ 8^{\frac{2}{3}} = (\sqrt[3]{8})^2 = 2^2 = 4 ]

幂函数的综合应用

幂函数的运算法则在代数化简、方程求解和函数分析中具有广泛应用。

• 化简表达式：利用幂法则简化复杂表达式。
• 求解方程：通过幂运算求解未知数。
• 科学计算：在物理、化学等领域中，幂函数用于表示指数增长或衰减。

常见错误与注意事项

在使用幂函数运算法则时,需注意以下几点：

1. 底数不能为零：零的负指数和零次幂无定义。
2. 指数运算优先级：遵循先乘方、后乘除、后加减的运算顺序。
3. 负底数的偶次幂：负底数的偶次幂为正数，奇次幂为负数。