幂函数图像及性质总结表格:幂函数图像及性质总结表格
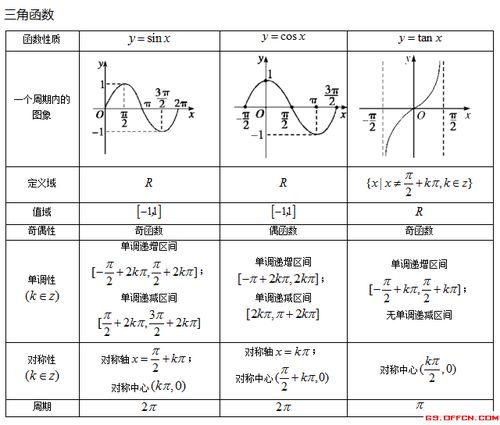
幂函数的定义
幂函数是指形如 ( y = x^a ) 的函数,( x ) 是自变量,( a ) 是常数(实数或复数),幂函数在数学分析、微积分、物理等领域有广泛应用。
幂函数的图像及性质总结
| 指数 ( a ) | 定义域 | 值域 | 单调性 | 奇偶性 | 图像特征 | 连续性 | 可导性 |
|---|---|---|---|---|---|---|---|
| ( a > 0 ) | ( \mathbb{R} ) | ( (0, +\infty) ) | 在 ( (0, +\infty) ) 上单调递增 | 当 ( a ) 为偶数时为偶函数,奇数时为奇函数 | 当 ( a ) 为正整数时,图像为抛物线;当 ( a ) 为分数时,图像为曲线 | 连续 | 可导 |
| ( a = 0 ) | ( \mathbb{R} \setminus {0} ) | ( {1} ) | 恒等于 1 | 偶函数 | 水平直线 ( y = 1 ) | 在 ( x \neq 0 ) 处连续 | 可导 |
| ( a < 0 ) | ( \mathbb{R} \setminus {0} ) | ( (0, +\infty) ) | 在 ( (0, +\infty) ) 上单调递减 | 当 ( a ) 为偶数时为偶函数,奇数时为奇函数 | 当 ( a ) 为负整数时,图像为双曲线;当 ( a ) 为负分数时,图像为曲线 | 在 ( x \neq 0 ) 处连续 | 可导 |
| ( a ) 为分数 | 视分母而定 | 视分子而定 | 视 ( a ) 而定 | 视 ( a ) 而定 | 曲线 | 连续 | 可导 |
幂函数的图像示例
- 当 ( a = 2 ):图像为开口向上的抛物线,顶点在原点。
- 当 ( a = -1 ):图像为双曲线,渐近线为坐标轴。
- 当 ( a = 0.5 ):图像为平方根曲线,定义域为 ( [0, +\infty) )。
幂函数的性质
- 单调性:当 ( a > 0 ) 时,幂函数在 ( (0, +\infty) ) 上单调递增;当 ( a < 0 ) 时,幂函数在 ( (0, +\infty) ) 上单调递减。
- 奇偶性:当 ( a ) 为整数时,若 ( a ) 为偶数,则幂函数为偶函数;若 ( a ) 为奇数,则幂函数为奇函数。
- 连续性:幂函数在定义域内连续。
- 可导性:幂函数在定义域内可导,且导数为 ( y' = a x^{a-1} )。
幂函数的应用
幂函数在数学、物理、经济学等领域有广泛应用,
- 描述物体的运动规律(如自由落体运动)。
- 分析经济学中的生产函数。
- 描述生物学中的种群增长模型。
幂函数是数学中一类基础且重要的函数,其图像和性质因指数 ( a ) 的不同而变化,掌握幂函数的图像和性质,有助于更好地理解函数的分析与应用,通过上述总结表格,可以快速回顾幂函数的核心内容。

相关文章:
文章已关闭评论!