幂函数图像及性质总结：幂函数图像及性质全面解析

幂函数是函数中一个重要的基本类型,其形式为：

y = x^α

x 是自变量，α 是常数（称为幂指数），幂函数在数学的多个领域都有广泛应用,理解其图像和性质对于掌握函数思想至关重要。

本文将对幂函数 y = x^α 的图像和性质进行总结。

幂函数的定义域

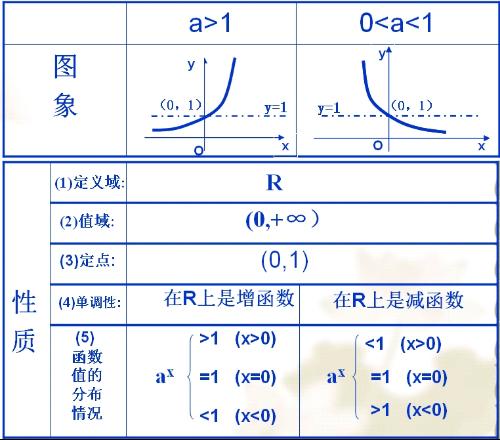
幂函数的定义域取决于指数 α 的值：

1. α 为正整数： 定义域为全体实数 R。
2. α 为零： y = x^0 = 1 (x ≠ 0)，定义域为 {x | x ≠ 0}。
3. α 为负整数： y = x^α = 1 / x^|α|，定义域为 {x | x ≠ 0}。
4. α 为正分数： 设 α = m/n (m, n 为互质的正整数，n > 1)，则定义域为 [0, +∞)。
5. α 为负分数： 设 α = m/n (m, n 为互质的整数，n > 0)，则定义域为 {x | x ≠ 0}。
6. α 为无理数： 定义域通常为 (0, +∞)。

幂函数的图像

幂函数的图像变化多样，主要取决于指数 α 的取值,以下是一些典型情况：

1. α > 0 (α 为正数)

   

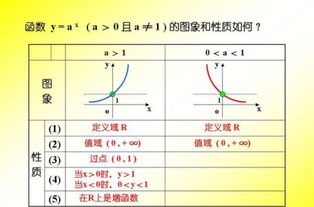
   • α = 1： y = x，图像为过原点 O(0,0) 和点 (1,1) 的直线，称为线性函数。
   • α = 2： y = x²，图像为抛物线，开口向上,顶点在原点。
   • α = 3： y = x³，图像为立方函数，过原点，关于原点中心对称,单调递增。
   • α > 0 且 α ≠ 1,2,3： 图像通常过原点 (0,0) 和 (1,1) 两点，当 0 < α < 1 时，图像在第一象限上是凹的，且当 x > 1 时，y 随 x 增大而增长速度减慢；当 α > 1 时，图像在第一象限上是凸的，且当 x > 1 时，y 随 x 增大而增长速度加快。α = 0.5 (y = √x)，α = 4 (y = x⁴)。

2. α = 0： y = x⁰ = 1 (x ≠ 0)，图像为除去点 (0,1) 外的水平直线 y=1。

3. α < 0 (α 为负数)

   • α = -1： y = x⁻¹ = 1/x，图像为双曲线，在第一、三象限,关于原点中心对称。
   • α = -2： y = x⁻² = 1/x²，图像为双曲线，在第一、二象限，y 轴对称。
   • α < 0 且 α ≠ -1： 图像通常不经过原点 (0,0)，当 x 从 0 增加到 +∞ 时，y 从 +∞ (或 -∞，取决于 α 的奇偶性) 减小到 0。α = -0.5 (y = 1/√x)，α = -3 (y = 1/x³)。

幂函数的性质

1. 单调性：

   

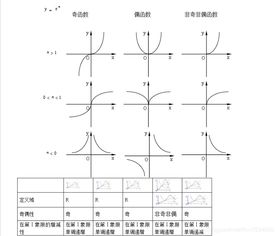
   • 当 α > 0 时，在定义域 (0, +∞) 上，函数 y = x^α 是单调递增的。α > β > 0，则 x^α > x^β (x > 1)；0 < α < β，则 x^α < x^β (x > 1)，在 (-∞, 0) 上，单调性取决于 α 的奇偶性：α 为奇数时递增，α 为偶数时递减。
   • 当 α < 0 时，在定义域 (0, +∞) 上，函数 y = x^α 是单调递减的，在 (-∞, 0) 上，单调性同样取决于 α 的奇偶性。
   • α = 0 时，函数为常数函数（在定义域内）,无单调性。

2. 奇偶性：

   • 偶函数： 如果对于定义域内所有 x，都有 f(-x) = f(x)，则函数为偶函数，图像关于 y 轴对称，幂函数中，当 α 为偶数时，y = x^α 是偶函数 (α=2,4,...)。
   • 奇函数： 如果对于定义域内所有 x，都有 f(-x) = -f(x)，则函数为奇函数，图像关于原点中心对称，幂函数中，当 α 为奇数时，y = x^α 是奇函数 (α=1,3,5,...)。
   • 非奇非偶： 当 α 既非整数也非零时，定义域通常不关于原点对称，或者即使对称，也未必满足奇偶函数的定义。α=0.5，定义域 [0,+∞),不关于原点对称。

3. 值域：

   • 取决于 α 和定义域。
   • α > 0：在 (0, +∞) 上，值域通常为 (0, +∞)；在 R 上，若 α 为奇数，值域为 R；若 α 为偶数，值域为 [0, +∞)。
   • α = 0：值域为 {1}。
   • α < 0：在 (0, +∞) 上，值域为 (0, +∞)；在 R 上，若 α 为奇数，值域为 (-∞, 0) ∪ (0, +∞)；若 α 为偶数，值域为 (0, +∞)。

4. 过定点：

   • 大多数幂函数都经过点 (1,1)，因为 1^α = 1。
   • 当 α > 0 时，也经过点 (0,0)。
   • α = 0 时，不经过 (0,0)。
   • α < 0 时，不经过 (0,0)。

5. 渐近线：

   • 当 α < 0 时，x=0 和 y=0 (即坐标轴) 通常是函数的垂直渐近线和水平渐近线。
   • 当 α > 0 且 α ≠ 整数时，在 x=0 处可能存在垂直渐近线或函数无定义，但 y=0 很少是渐近线。

幂函数 y = x^α 的性质和图像随 α 的变化而呈现显著差异，理解 α 的正负、有理数（特别是分母）以及零对定义域、单调性、奇偶性、图像形状（如过原点、凹凸性、渐近线）都有重要影响，掌握这些基本的图像和性质，是进一步学习更复杂函数（如指数函数、对数函数）以及解决相关应用问题的基础。