指数函数与对数函数的转换：指数函数与对数函数的转换

指数函数与对数函数的基本概念

指数函数

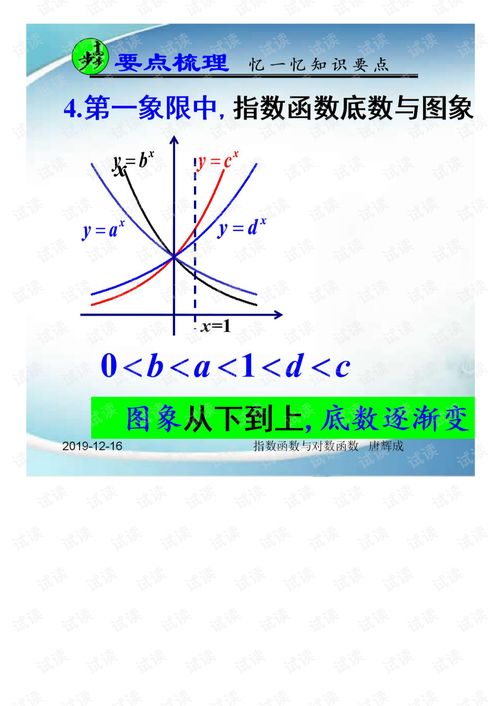
指数函数的一般形式为 ( y = a^x )，( a > 0 ) 且 ( a \neq 1 )，当 ( a > 1 ) 时，函数单调递增；当 ( 0 < a < 1 ) 时，函数单调递减，指数函数的图像通常呈“指数增长”或“指数衰减”的趋势。

对数函数

对数函数是指数函数的逆运算，其一般形式为 ( y = \log_a x )，( a > 0 ) 且 ( a \neq 1 )，( x > 0 )，对数函数的定义域为正实数，值域为全体实数，对数函数与指数函数互为反函数，它们的图像关于直线 ( y = x ) 对称。

指数函数与对数函数的转换关系

指数函数与对数函数之间存在密切的联系。( y = a^x )，则 ( x = \log_a y )，反之，( y = \log_a x )，则 ( x = a^y )，这种关系使得我们可以通过指数函数的性质来研究对数函数,反之亦然。

基本转换公式

设 ( y = a^x )，则 ( x = \log_a y )，这一关系表明，指数函数的自变量 ( x ) 可以表示为对数函数的值，同样地，对数函数的自变量 ( x ) 可以表示为指数函数的值。

转换公式的推导

假设 ( y = a^x )，则两边取以 ( a ) 为底的对数，得到 ( \log_a y = \log_a (a^x) = x )。( x = \log_a y ),这证明了指数函数与对数函数之间的直接转换关系。

转换公式的应用

解方程

通过转换公式，我们可以解决一些复杂的方程，解方程 ( 2^x = 8 )。

根据转换公式，( x = \log_2 8 )，由于 ( 2^3 = 8 )，( x = 3 )。

化简表达式

在化简表达式时，转换公式也非常有用，化简 ( \log_2 (8 \times 4) )。

根据对数的性质，( \log_2 (8 \times 4) = \log_2 8 + \log_2 4 = 3 + 2 = 5 )。

函数图像分析

通过转换公式，我们可以分析两个函数的图像关系，函数 ( y = 2^x ) 与 ( y = \log_2 x ) 关于直线 ( y = x ) 对称。

实际应用

科学计算

在科学计算中，指数函数和对数函数广泛应用于描述自然现象，如放射性衰变、人口增长、地震强度等，通过转换公式,我们可以将问题转化为更易于处理的形式。

数据分析

在数据分析中，对数函数常用于处理大规模数据，使其符合正态分布，在统计学中,常用对数转换来分析数据的分布趋势。

指数函数与对数函数之间的转换关系是数学中的重要基础，通过掌握这一关系，我们可以更灵活地解决数学问题，理解函数的性质，并在实际应用中发挥其作用，无论是解方程、化简表达式，还是分析函数图像,转换公式都是不可或缺的工具。

希望本文能帮助读者更好地理解指数函数与对数函数之间的转换关系,并在学习和应用中取得更好的效果。