欧拉函数定义：欧拉函数的定义与理解

欧拉函数,也称为欧拉 totient 函数，是数论中一个重要的函数，它由数学家莱昂哈德·欧拉在研究与整数互质的整数个数时引入，欧拉函数的定义如下：

欧拉函数 φ(n) 定义为：对于正整数 n，φ(n) 表示小于等于 n 的正整数中与 n 互质的数的个数。

两个数如果除了 1 以外没有其他公因数，则称这两个数互质，1 和任何数互质，而 2 和 3 互质，但 2 和 4 不互质。

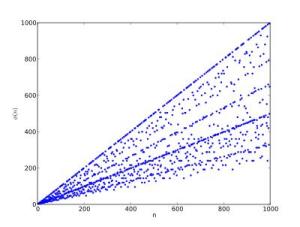
欧拉函数的计算示例

以 n=1 为例：
φ(1) = 1（因为 1 与 1 互质，所以结果为 1）。

以 n=2 为例：
小于等于 2 的正整数有 1 和 2。
1 与 2 互质，2 与 2 不互质，φ(2) = 1。

以 n=4 为例：
小于等于 4 的正整数有 1、2、3、4。
1 与 4 互质，2 与 4 不互质，3 与 4 互质，4 与 4 不互质，φ(4) = 2。

欧拉函数的基本性质

1. 积性函数：m 和 n 互质，则 φ(mn) = φ(m) × φ(n)。
   φ(6) = φ(2) × φ(3) = 1 × 2 = 2。

   

2. 质数的欧拉函数：n 是质数，则 φ(n) = n - 1。
   φ(7) = 6。

3. 完全平方数的欧拉函数：n 是完全平方数，则 φ(n) ≤ n/2。

4. 欧拉定理：a 和 n 互质，则 a^{φ(n)} ≡ 1 (mod n)。
   这一定理在密码学中有着广泛的应用。

欧拉函数的应用

欧拉函数在数论、密码学、计算机科学等领域有广泛应用。

• 在 RSA 加密算法中，欧拉函数用于计算模数的 φ(n)，以生成公钥和私钥。
• 在图论中,欧拉函数用于计算欧拉回路的条件。
• 在算法设计中,欧拉函数用于快速计算与某个数互质的数的个数。