高斯函数的傅里叶变换：高斯函数的傅里叶变换，完美对称与无限应用

高斯函数的定义

高斯函数的一般形式为：

[ g(x) = e^{-\pi x^2} ]

这是标准高斯函数，其均值为0，标准差为1,更一般的形式为：

[ g(x) = e^{-(x - \mu)^2 / (2\sigma^2)} ]

(\mu) 是均值，(\sigma) 是标准差。

傅里叶变换的定义

傅里叶变换将信号从时域（或空域）转换到频域,其定义为：

[ G(f) = \int_{-\infty}^{\infty} g(x) e^{-2\pi i f x} dx ]

对于高斯函数,我们通常使用标准形式进行变换。

高斯函数的傅里叶变换推导

考虑标准高斯函数：

[ g(x) = e^{-\pi x^2} ]

其傅里叶变换为：

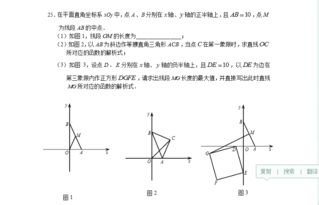
[ G(f) = \int_{-\infty}^{\infty} e^{-\pi x^2} e^{-2\pi i f x} dx ]

为了计算这个积分，我们可以使用高斯积分的技巧,令：

[ u = x + i f ]

则：

[ G(f) = \int_{-\infty}^{\infty} e^{-\pi (x + i f)^2} dx ]

通过复变函数的积分方法,可以证明：

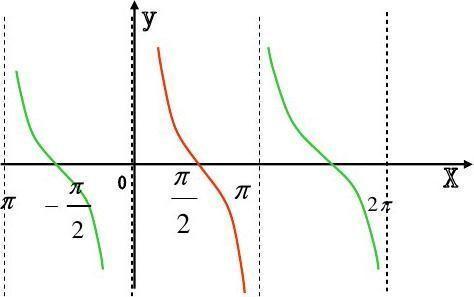
[ G(f) = e^{-\pi f^2} ]

高斯函数的傅里叶变换仍然是一个高斯函数，且其形状和宽度与原函数相同,只是频率变量发生了变化。

傅里叶变换的性质

高斯函数的傅里叶变换具有以下重要性质：

1. 自相似性：高斯函数的傅里叶变换仍然是高斯函数,且形状相同。
2. 能量守恒：高斯函数在时域和频域中的能量相同。
3. 无限可分离性：高斯函数在时域和频域中都是最“紧凑”的函数,具有最小不确定性。

应用领域

信号处理

在信号处理中，高斯函数的傅里叶变换常用于滤波器设计、频谱分析和信号去噪,高斯滤波器因其平滑特性被广泛应用于图像处理中。

图像处理

在图像处理中，高斯函数用于实现高斯模糊，这是一种常用的图像平滑技术，高斯函数的傅里叶变换在频域中表现为低通滤波器,能够有效去除图像中的高频噪声。

量子力学

在量子力学中，高斯波包的演化可以用高斯函数的傅里叶变换来描述,高斯函数在位置空间和动量空间的表示分别对应于粒子的位置分布和动量分布。

统计学

高斯函数在统计学中代表正态分布,其傅里叶变换在信号处理和概率论中具有重要意义。

高斯函数的傅里叶变换不仅在数学上具有简洁的形式，还在众多科学和工程领域中发挥着重要作用，其自相似性和能量守恒的特性使其成为信号处理、图像处理和量子力学等领域不可或缺的工具，通过对高斯函数傅里叶变换的深入理解，我们可以更好地掌握信号的频域特性,从而设计出更高效的算法和系统。