三角函数特殊角值：轻松掌握三角函数特殊角值，记忆与应用指南

来源：网络作者：日期：2025-10-29 23:14:28

在学习三角函数的过程中，掌握特殊角（或标准角）的三角函数值是基础中的基础，这些角度的正弦、余弦、正切等函数值具有特定的规律，是解决更复杂三角问题的“钥匙”，本文将介绍常见的特殊角及其三角函数值,并提供一些记忆和应用的技巧。

什么是三角函数的特殊角？

特殊角通常指的是那些在几何图形中具有特殊意义，或者其三角函数值可以通过几何方法（如单位圆、特殊三角形）精确计算出来的角度，在标准的度数制下,最常用的特殊角有：

0°, 30°, 45°, 60°, 90° （以及它们的补角和诱导角，如 180°, 150°, 135°, 120° 等,因为它们的函数值可以通过诱导公式从这些基础角推导出来）

特殊角的三角函数值

三角函数特殊角值：轻松掌握三角函数特殊角值，记忆与应用指南

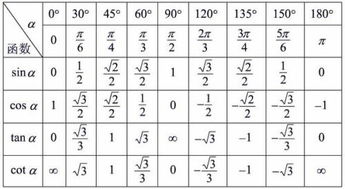
以下是这些特殊角的六个基本三角函数值（正弦 sin、余弦 cos、正切 tan、余切 cot、正割 sec、余割 csc）的表格，这些值是精确值,通常用根号表示。

| 角度 (度) | 角度 (弧度) | sin θ | cos θ | tan θ | cot θ | sec θ | csc θ | | ：-------- | :---------- | :---- | :---- | :---- | :---- | :---- | :---- | | 0° | 0 | 0 | 1 | 0 | | 1 | | | 30° | π/6 | 1/2 | √3/2 | 1/√3 | √3 | 2 | 2/√3 | | 45° | π/4 | √2/2 | √2/2 | 1 | 1 | √2 | √2 | | 60° | π/3 | √3/2 | 1/2 | √3 | 1/√3 | 2/√3 | 2 | | 90° | π/2 | 1 | 0 | | 0 | | 1 |

记忆技巧

三角函数特殊角值：轻松掌握三角函数特殊角值，记忆与应用指南

记住这些值,可以尝试以下方法：

理解与推导：
- 0° 和 90°： 单位圆上，0° 对应点 (1, 0)，cos0°=1, sin0°=0；90° 对应点 (0, 1)，cos90°=0, sin90°=1，tan0°=0/sin0°=0/0 无定义（但极限为0），tan90°=sin90°/cos90°=1/0 无定义。
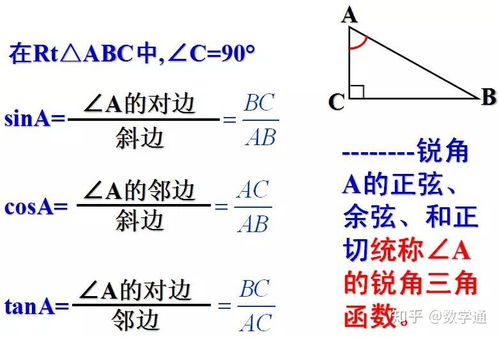
- 30° 和 60°： 对应 30-60-90 特殊三角形，该三角形的边长比例为 1 : √3 : 2，对于 30° 角，对边是斜边的一半，邻边是斜边的 √3/2，利用 sin = 对边/斜边，cos = 邻边/斜边，tan = 对边/邻边,可以推导出值。
- 45°： 对应 45-45-90 特殊三角形，该三角形的边长比例为 1 : 1 : √2，对边和邻边相等，sin45°=cos45°=√2/2，tan45°=1。
口诀记忆：
- 对于 sin 值： 0°, 30°, 45°, 60°, 90° 的 sin 值可以看作是 0, 1/2, √2/2, √3/2, 1，可以想象分子是 0, 1, √2, √3, 2 的平方根形式，分母是 2。
- 对于 cos 值： cos 值是 sin 值的倒序：1, √3/2, √2/2, 1/2, 0。
- 对于 tan 值： tan = sin/cos，tan0°=0, tan30°= (1/2)/(√3/2)=1/√3, tan45°=1, tan60°=√3, tan90° 无定义，可以记为 0, 1/√3, 1, √3, 无。
单位圆记忆： 在单位圆上，特殊角的终边与 x 轴的夹角，其坐标 (cosθ, sinθ) 就是该角的余弦和正弦值，想象单位圆上的这些点,可以帮助记忆。