正切函数的诱导公式：正切函数诱导公式的应用与推导

诱导公式的定义

诱导公式是指将任意角的三角函数值转化为锐角三角函数值的公式,对于正切函数，诱导公式主要包括以下几类：

1. 角度加减2π的公式：
   [ \tan(\theta + 2k\pi) = \tan\theta, \quad k \in \mathbb{Z} ]

2. 角度加减π的公式：
   [ \tan(\theta + \pi) = \tan\theta, \quad \tan(\theta - \pi) = \tan\theta ]

3. 角度加减π/2的公式：
   [ \tan\left(\frac{\pi}{2} + \theta\right) = -\cot\theta, \quad \tan\left(\frac{\pi}{2} - \theta\right) = \cot\theta ]

4. 角度加减π/4的公式：
   [ \tan\left(\frac{\pi}{4} + \theta\right) = \frac{1 + \tan\theta}{1 - \tan\theta}, \quad \tan\left(\frac{\pi}{4} - \theta\right) = \frac{1 - \tan\theta}{1 + \tan\theta} ]

5. 角度加减π/3、π/6等特殊角的公式：
   这些公式通常通过单位圆或三角恒等式推导得出。

诱导公式的推导

角度加减2π的公式

正切函数的周期为π，即每增加或减少π，函数值不变，但2π是正切函数的周期吗？正切函数的周期是π，

[ \tan(\theta + 2k\pi) = \tan\theta, \quad k \in \mathbb{Z} ]

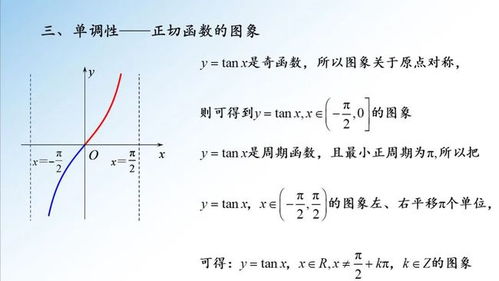
这是因为2π是正弦和余弦函数的周期，而正切函数是正弦与余弦的比值，因此也具有2π的周期性。

角度加减π的公式

由于正切函数的周期为π，

[ \tan(\theta + \pi) = \tan\theta, \quad \tan(\theta - \pi) = \tan\theta ]

角度加减π/2的公式

考虑角度(\frac{\pi}{2} + \theta)，其终边位于第二象限，此时正切函数值为负，且与余切函数相关：

[ \tan\left(\frac{\pi}{2} + \theta\right) = -\cot\theta ]

同理,对于(\frac{\pi}{2} - \theta)：

[ \tan\left(\frac{\pi}{2} - \theta\right) = \cot\theta ]

角度加减π/4的公式

考虑角度(\frac{\pi}{4} + \theta)，其正切值可以通过正切加法公式推导：

[ \tan\left(\frac{\pi}{4} + \theta\right) = \frac{\tan\frac{\pi}{4} + \tan\theta}{1 - \tan\frac{\pi}{4} \cdot \tan\theta} = \frac{1 + \tan\theta}{1 - \tan\theta} ]

同理,对于(\frac{\pi}{4} - \theta)：

[ \tan\left(\frac{\pi}{4} - \theta\right) = \frac{1 - \tan\theta}{1 + \tan\theta} ]

角度加减π/3、π/6等特殊角的公式

这些公式通常通过单位圆或三角恒等式推导,对于(\frac{\pi}{3} + \theta)：

[ \tan\left(\frac{\pi}{3} + \theta\right) = \frac{\tan\frac{\pi}{3} + \tan\theta}{1 - \tan\frac{\pi}{3} \cdot \tan\theta} = \frac{\sqrt{3} + \tan\theta}{1 - \sqrt{3} \tan\theta} ]

诱导公式的记忆方法

1. 奇变偶不变：角度中的π的倍数如果是奇数倍，则函数名改变（正弦变余弦，余弦变正弦，正切不变）；如果是偶数倍，则函数名不变。

2. 符号看象限：将角度化为锐角后，根据原角所在象限确定符号。

应用示例

例1：求(\tan\left(\frac{5\pi}{4}\right))的值。

解：
(\frac{5\pi}{4} = \pi + \frac{\pi}{4})，

[ \tan\left(\frac{5\pi}{4}\right) = \tan\left(\pi + \frac{\pi}{4}\right) = \tan\frac{\pi}{4} = 1 ]

例2：求(\tan\left(\frac{3\pi}{4}\right))的值。

解：
(\frac{3\pi}{4} = \frac{\pi}{2} + \frac{\pi}{4})，

[ \tan\left(\frac{3\pi}{4}\right) = \tan\left(\frac{\pi}{2} + \frac{\pi}{4}\right) = -\cot\frac{\pi}{4} = -1 ]