指数函数的基本公式：指数函数的基本公式及其应用解析

指数函数是数学中一类重要的函数形式，广泛应用于自然科学、经济学、金融学等领域，其核心特征在于函数值随自变量的变化呈指数增长或衰减，本文将围绕指数函数的基本公式展开，深入探讨其定义、性质及实际应用。

指数函数的定义

指数函数的一般形式为：

[ f(x) = a^x ]

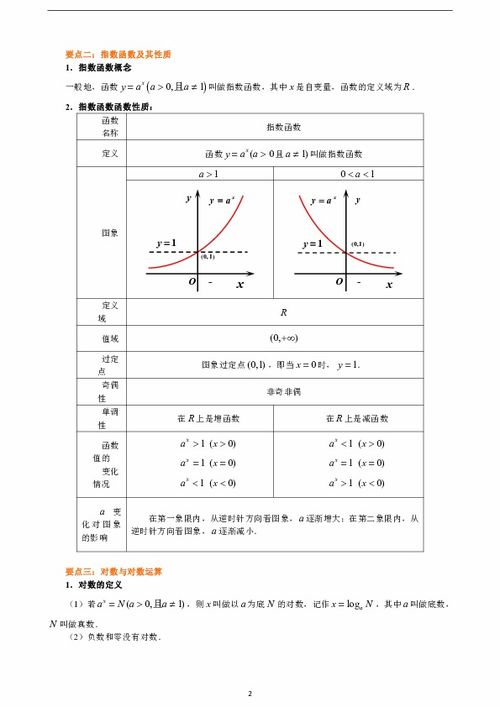
( a ) 是底数，( x ) 是指数，底数 ( a ) 必须满足 ( a > 0 ) 且 ( a \neq 1 )，当 ( a = 1 ) 时，函数恒等于 1，失去了指数变化的意义；当 ( a \leq 0 ) 时，函数在实数范围内可能无定义或产生振荡，因此底数 ( a ) 的取值范围为 ( (0, +\infty) ) 且 ( a \neq 1 )。

指数函数的基本公式

1. 定义公式
   [ f(x) = a^x ] 这是指数函数的最基本形式，( a ) 是底数，( x ) 是指数。

2. 特殊底数的指数函数

   

   • 当 ( a = e )（自然对数的底数，约等于 2.71828）时，函数为 ( f(x) = e^x )，称为自然指数函数。
   • 当 ( a = 10 ) 时，函数为 ( f(x) = 10^x ),称为常用指数函数。

3. 指数函数的运算性质

   • 乘法法则：( a^m \cdot a^n = a^{m+n} )
   • 幂的乘方法则：( (a^m)^n = a^{mn} )
   • 幂的乘方法则（不同底数）：( a^m \cdot b^m = (ab)^m )
   • 分数指数法则：( a^{m/n} = \sqrt[n]{a^m} )

4. 指数函数的导数公式
   指数函数的导数是其自身乘以自然对数的底数 ( e ) 的自然对数，即：
   [ \frac{d}{dx} a^x = a^x \ln a ] 当底数 ( a = e ) 时，导数简化为：
   [ \frac{d}{dx} e^x = e^x ]

5. 指数函数的积分公式
   指数函数的积分公式为：
   [ \int a^x \, dx = \frac{a^x}{\ln a} + C ] ( C ) 是积分常数。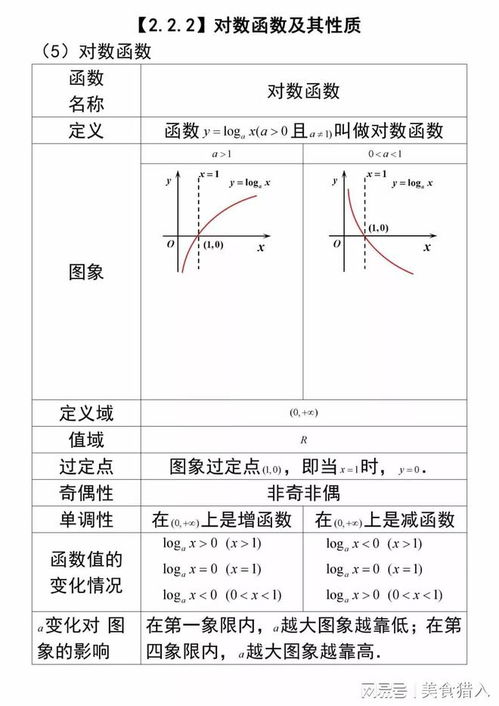

   

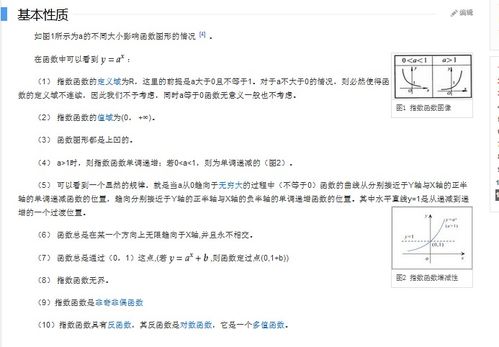
指数函数的图像与性质

• 单调性：当 ( a > 1 ) 时，函数单调递增；当 ( 0 < a < 1 ) 时，函数单调递减。
• 过定点：所有指数函数均经过点 ( (0, 1) )，因为 ( a^0 = 1 )。
• 渐近线：当 ( x \to -\infty ) 时，若 ( a > 1 )，函数值趋近于 0；若 ( 0 < a < 1 )，函数值趋近于正无穷。
• 对称性：指数函数与对数函数互为反函数，其图像关于直线 ( y = x ) 对称。

指数函数的应用

1. 复利计算
   在金融学中，复利公式为：
   [ A = P \left(1 + \frac{r}{n}\right)^{nt} ] ( A ) 是未来价值，( P ) 是本金，( r ) 是年利率，( n ) 是复利频率，( t ) 是时间。

2. 放射性衰变
   放射性物质的衰变规律可以用指数函数描述：
   [ N(t) = N_0 e^{-\lambda t} ] ( N(t) ) 是时间 ( t ) 时的剩余原子数，( N_0 ) 是初始原子数，( \lambda ) 是衰变常数。

3. 人口增长模型
   在生态学中，指数增长模型为：
   [ P(t) = P_0 e^{rt} ] ( P(t) ) 是时间 ( t ) 时的人口数量，( P_0 ) 是初始人口，( r ) 是增长率。

指数函数的基本公式是理解其性质和应用的基础，通过掌握定义、运算性质、导数和积分公式，可以更好地解决实际问题，无论是金融计算、物理建模还是生物学中的增长问题，指数函数都扮演着不可或缺的角色，希望本文能帮助读者深入理解指数函数的核心概念,并灵活运用于实际场景中。