random函数的原理：random函数的原理，从数学到实现

什么是随机性？

在数学和计算机科学中,真正的随机性（True Randomness）通常来自于不可预测的物理过程，例如大气噪声、放射性衰变等，计算机是确定性系统，无法直接生成真正的随机数，random函数通常生成的是伪随机数（Pseudo-Random Numbers），即通过确定性算法生成的序列，这些序列在统计上表现出随机性，但实际上是可重复的。

随机数生成器的实现方式

硬件随机数生成器

硬件随机数生成器（HRNG）利用物理现象（如电子噪声、热噪声等）来生成真正的随机数，这种方式生成的随机数不可预测，且通过统计测试后通常被认为是高质量的随机数，硬件随机数生成器依赖于外部设备，速度较慢，且在某些嵌入式系统或资源受限的环境中难以使用。

软件随机数生成器

软件随机数生成器（Software RNG）通过数学算法生成伪随机数序列，这类生成器速度快、资源占用少，广泛应用于编程语言的标准库中，常见的伪随机数生成算法包括线性同余生成器（LCG）、梅森旋转算法（Mersenne Twister）等。

伪随机数生成算法

线性同余生成器（LCG）

LCG是最简单的伪随机数生成算法之一,其公式如下：

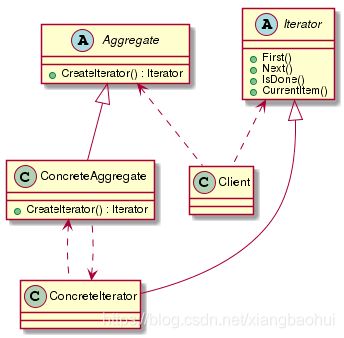
[ X_{n+1} = (a \times X_n + c) \mod m ]

(X_n) 是当前随机数，(a)、(c) 和 (m) 是常数，分别称为乘数、增量和模数，虽然LCG实现简单，但其生成的随机序列存在周期短、分布不均匀等问题，因此在现代编程语言中已逐渐被更高级的算法取代。

梅森旋转算法（Mersenne Twister）

梅森旋转算法是一种更复杂的伪随机数生成算法,由日本科学家井上盛久于1997年提出，该算法的周期可达 (2^{19937}-1)，是目前已知最长的伪随机数生成周期之一，Mersenne Twister在统计性能、速度和内存占用之间取得了良好的平衡，因此被广泛应用于Python、C++等语言的标准库中。

随机种子（Seed）

伪随机数生成器的初始值称为种子（Seed），种子决定了随机数序列的起始点，如果使用相同的种子，生成器将产生完全相同的随机数序列，在需要可重复性的实验或测试中，设置种子是一个重要的步骤，在机器学习中，为了确保实验结果的可复现性，常常会在训练模型前设置随机种子。

random函数的局限性

尽管伪随机数生成器在大多数情况下表现良好,但它们并非完美，常见的问题包括：

1. 周期性：如果生成器的周期不够长，可能会在短时间内重复生成相同的随机数。
2. 分布不均匀：某些算法生成的随机数在某些区间内可能过于密集或稀疏。
3. 可预测性：如果伪随机数生成器的算法不够复杂，攻击者可能通过部分已知的随机数序列推断出生成器的状态，进而预测未来的随机数。

实际应用中的建议

1. 选择合适的随机数生成器：根据应用场景选择合适的算法，对于一般用途，Mersenne Twister是一个安全的选择；对于密码学应用，需要使用更安全的随机数生成器（如Cryptographically Secure Pseudo-Random Number Generator, CSPRNG）。
2. 设置种子：在需要可重复性的情况下，设置种子可以确保结果的一致性。
3. 避免常见错误：不要使用时间戳作为种子，因为时间戳通常不够随机；避免在循环中使用随机数作为决策条件，这可能导致某些结果被过度选择。