指数函数和幂函数:指数函数与幂函数,数学中的两种重要函数
基本概念
指数函数
指数函数是指函数形式为 ( f(x) = a^x ) 的函数,( a > 0 ) 且 ( a \neq 1 ),这里的 ( a ) 称为底数,( x ) 是自变量,称为指数,指数函数的定义域为全体实数,值域为 ( (0, +\infty) )。
幂函数
幂函数是指函数形式为 ( f(x) = x^a ) 的函数,( a ) 是常数,称为指数或幂,幂函数的定义域和值域取决于指数 ( a ) 的取值,例如当 ( a ) 为整数时,定义域为全体实数;当 ( a ) 为分数时,定义域可能受到限制。
指数函数的详细分析
定义与图像
指数函数 ( f(x) = a^x ) 的图像取决于底数 ( a ) 的取值:
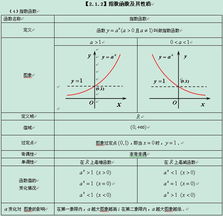
- 若 ( a > 1 ),函数单调递增,且当 ( x ) 趋近于负无穷时,函数值趋近于 0;当 ( x ) 趋近于正无穷时,函数值趋近于无穷大。
- 若 ( 0 < a < 1 ),函数单调递减,且当 ( x ) 趋近于负无穷时,函数值趋近于无穷大;当 ( x ) 趋近于正无穷时,函数值趋近于 0。
性质
- 单调性:当 ( a > 1 ) 时,函数单调递增;当 ( 0 < a < 1 ) 时,函数单调递减。
- 极限:当 ( x \to +\infty ) 时,若 ( a > 1 ),则 ( a^x \to +\infty );若 ( 0 < a < 1 ),则 ( a^x \to 0 )。
- 导数:指数函数的导数为 ( f'(x) = a^x \ln a ),这表明其增长率与自身函数值成正比。
应用
指数函数在科学、金融和工程等领域有广泛应用,复利计算、人口增长模型、放射性衰变等都可以用指数函数来描述。
幂函数的详细分析
定义与图像
幂函数 ( f(x) = x^a ) 的图像取决于指数 ( a ) 的取值:
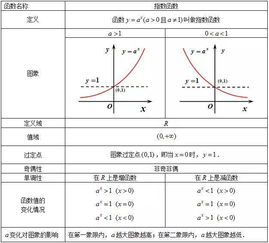
- 若 ( a ) 为正整数,函数在 ( x > 0 ) 时单调递增,且图像通过原点。
- 若 ( a ) 为负整数,函数在 ( x \neq 0 ) 时单调递减,且图像关于原点对称。
- 若 ( a ) 为分数,函数的定义域和单调性会根据分母的奇偶性有所不同。
性质
- 单调性:幂函数的单调性取决于指数 ( a ) 的符号和大小。
- 极限:当 ( x \to +\infty ) 时,若 ( a > 0 ),则 ( x^a \to +\infty );若 ( a < 0 ),则 ( x^a \to 0 )。
- 导数:幂函数的导数为 ( f'(x) = a x^{a-1} ),这在求解变化率问题时非常有用。
应用
幂函数在物理学、经济学和统计学中有着广泛的应用,速度与时间的关系、能量与质量的关系(如爱因斯坦的质能方程 ( E = mc^2 ))、以及幂律分布等。
指数函数与幂函数的比较
| 特点 | 指数函数 ( f(x) = a^x ) | 幂函数 ( f(x) = x^a ) |
|---|---|---|
| 自变量位置 | 指数位置 | 底数位置 |
| 定义域 | 全体实数 | 取决于 ( a ) |
| 增长速度 | 快速增长(当 ( a > 1 )) | 增长速度取决于 ( a ) |
| 图像 | 通常为指数增长曲线 | 取决于 ( a ) 的取值 |
| 应用领域 | 金融、生物学、物理学等 | 物理学、经济学、统计学等 |
指数函数和幂函数是数学中两类基础且重要的函数,它们在定义、性质和应用上各有特点,但都广泛应用于科学、工程和经济领域,理解这两类函数的区别与联系,不仅有助于数学学习,也能帮助我们在实际问题中选择合适的数学工具进行建模和分析。
无论是指数函数的快速增长,还是幂函数的多样化表现,它们都展现了数学在描述现实世界中的强大能力,通过深入学习和应用,我们可以更好地理解和解决实际问题。
相关文章:
文章已关闭评论!