特殊的三角函数值表:特殊角的三角函数值表及其应用
特殊角的三角函数值表
特殊角的三角函数值通常可以通过几何图形(如等边三角形、等腰直角三角形)或单位圆推导得出,以下是几个常见特殊角的三角函数值表:
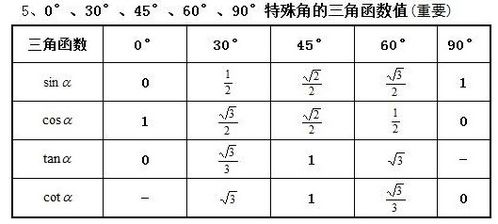
| 角度(度) | 角度(弧度) | sinθ | cosθ | tanθ |
|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0 |
| 30° | π/6 | 1/2 | √3/2 | 1/√3 |
| 45° | π/4 | √2/2 | √2/2 | 1 |
| 60° | π/3 | √3/2 | 1/2 | √3 |
| 90° | π/2 | 1 | 0 | 无定义 |
| 180° | 0 | -1 | 0 |
特殊角三角函数值的推导方法
30°和60°的推导
通过等边三角形分割为两个30°-60°-90°的直角三角形,可以得到sin30°=1/2,cos30°=√3/2,sin60°=√3/2,cos60°=1/2。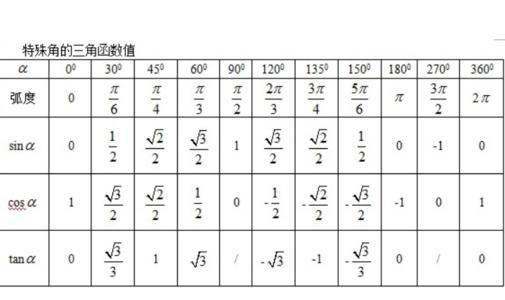
45°的推导
通过等腰直角三角形,可以得到sin45°=cos45°=√2/2,tan45°=1。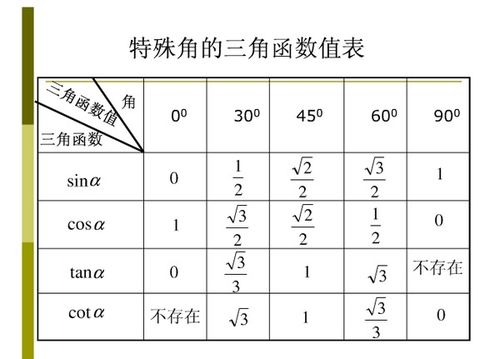
0°和90°的推导
0°是单位圆上x轴正方向的角,其正弦值为0,余弦值为1;90°是y轴正方向的角,正弦值为1,余弦值为0。
记忆技巧
为了方便记忆,可以使用以下方法:
- “头法则”:对于30°、45°、60°的正弦值,分子分别为1、√2、√3,分母均为2。
- “分母法则”:余弦值与正弦值互换,正切值等于正弦除以余弦。
应用示例
例题:求sin15°的值。
解法:
sin15° = sin(45° - 30°) = sin45°cos30° - cos45°sin30°
= (√2/2)(√3/2) - (√2/2)(1/2)
= (√2/2)( (√3 - 1)/2 )
= (√2(√3 - 1))/4
相关文章:
文章已关闭评论!