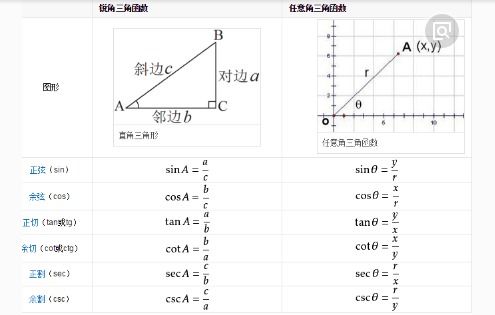
任意三角函数的计算方法：任意三角函数的计算方法

本文目录导读：

1. 泰勒级数展开法
2. 恒等式转换法
3. 查表法
4. 计算器与计算机软件

泰勒级数展开法

泰勒级数展开是计算三角函数的一种常用方法，尤其适用于计算机编程和数值计算，其基本思想是将三角函数表示为无穷级数的形式,通过截断级数来近似计算函数值。

正弦函数的泰勒级数展开为：

[ \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots ]

余弦函数的泰勒级数展开为：

[ \cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots ]

(x)为弧度制的角度值，通过取级数的前几项,可以得到足够精确的近似值。

恒等式转换法

利用三角恒等式可以将复杂的三角函数转化为更简单的形式，通过角度加法公式，可以将任意角度的三角函数分解为已知角度（如0°、30°、45°、60°、90°等）的组合。

计算(\sin(75^\circ))：

[ \sin(75^\circ) = \sin(45^\circ + 30^\circ) = \sin(45^\circ)\cos(30^\circ) + \cos(45^\circ)\sin(30^\circ) ]

代入已知值：

[ \sin(45^\circ) = \cos(45^\circ) = \frac{\sqrt{2}}{2}, \quad \sin(30^\circ) = \frac{1}{2}, \quad \cos(30^\circ) = \frac{\sqrt{3}}{2} ]

计算得：

[ \sin(75^\circ) = \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2} + \frac{\sqrt{2}}{2} \cdot \frac{1}{2} = \frac{\sqrt{6} + \sqrt{2}}{4} ]

这种方法适用于角度为特殊角或其组合的情况。

查表法

在早期计算工具不发达的时代，查表法是一种常用的三角函数计算方法，通过预先计算并整理出常见角度的三角函数值，用户可以直接查表得到结果，虽然现代计算工具已经普及,但查表法在某些场合仍具有参考价值。

计算器与计算机软件

现代计算器和计算机软件（如Python的math库、MATLAB、Excel等）可以快速准确地计算任意角度的三角函数值，这些工具通常采用泰勒级数或其他数值方法进行内部计算,用户只需输入角度值即可得到结果。

任意三角函数的计算方法多种多样，选择哪种方法取决于具体的应用场景和精度要求，泰勒级数展开适用于高精度计算，恒等式转换适用于特殊角度，查表法适用于快速查询,而计算器和计算机软件则提供了最便捷的解决方案。

在实际应用中，建议根据需求选择合适的方法,并注意计算精度和效率的平衡。