配对样本t检验(配对样本t检验需要正态性检验吗)
配对样本t检验在数据分析中的应用与优势
在统计学中,配对样本t检验是一种常用的假设检验方法,主要用于比较两个相关样本的均值是否存在显著差异,在实际应用中,配对样本t检验在医学、心理学、教育学等领域发挥着重要作用,本文将介绍配对样本t检验的基本原理、应用场景以及优势,以期为相关领域的学者和实践者提供参考。
配对样本t检验的基本原理
配对样本t检验是一种基于t分布的假设检验方法,其基本原理如下:
提出假设:假设检验分为原假设(H0)和备择假设(H1),在配对样本t检验中,原假设为两个相关样本的均值相等,即μ1 = μ2;备择假设为两个相关样本的均值不相等,即μ1 ≠ μ2。
计算检验统计量:根据配对样本的数据,计算t值,t值是样本均值之差除以标准误的比值,公式如下:
t = (x1 - x2) / SE
x1和x2分别为两个相关样本的均值,SE为标准误。
确定临界值:根据自由度和显著性水平,查找t分布表,得到临界值。
比较检验统计量与临界值:如果检验统计量大于临界值,则拒绝原假设,认为两个相关样本的均值存在显著差异;反之,则接受原假设。
配对样本t检验的应用场景
医学领域:在临床试验中,配对样本t检验可用于比较两种药物或治疗方法的效果差异。
心理学领域:在心理实验中,配对样本t检验可用于比较同一个人在不同时间点的心理状态变化。
教育学领域:在教育研究中,配对样本t检验可用于比较同一组学生在不同教学方式下的学习成绩差异。
工程领域:在产品测试中,配对样本t检验可用于比较两个不同批次产品的质量差异。
配对样本t检验的优势
考虑样本相关性:配对样本t检验考虑了样本之间的相关性,提高了检验的准确性。
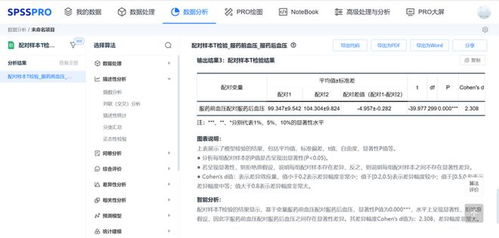
提高效率:与独立样本t检验相比,配对样本t检验所需样本量更小,提高了检验效率。
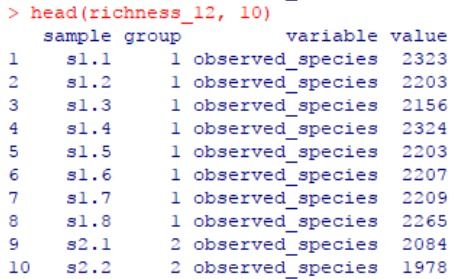
降低误差:配对样本t检验能够有效降低随机误差,提高检验结果的可靠性。
广泛应用:配对样本t检验在多个领域均有广泛应用,具有很高的实用价值。
配对样本t检验是一种在数据分析中具有重要意义的假设检验方法,通过对配对样本t检验的基本原理、应用场景以及优势的介绍,本文旨在为相关领域的学者和实践者提供参考,在实际应用中,应根据具体问题选择合适的检验方法,以提高数据分析的准确性和可靠性。
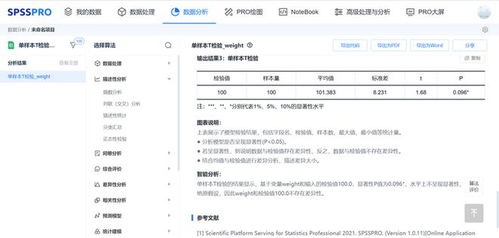
相关文章:
文章已关闭评论!










