三角函数的转换公式大全：三角函数转换公式大全，从基础到进阶的全面解析

三角函数转换公式大全：从基础到进阶的全面解析

三角函数是数学中重要的函数之一，广泛应用于几何、物理、工程等领域，在解决三角函数相关问题时，转换公式是必不可少的工具，本文将系统地介绍三角函数的转换公式，包括诱导公式、同角关系公式、和差角公式、倍角公式、半角公式以及和差化积公式等,帮助读者全面掌握三角函数的转换技巧。

诱导公式

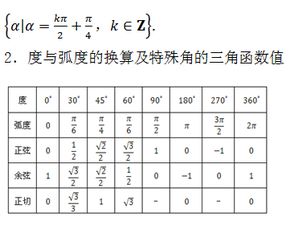
诱导公式用于将任意角的三角函数值转化为锐角三角函数值,是三角函数转换的基础。

1. 角与π的整数倍关系：

   • sin(π + α) = -sinα
   • cos(π + α) = -cosα
   • tan(π + α) = tanα

2. 角与π/2的奇数倍关系：

   • sin(π/2 + α) = cosα
   • cos(π/2 + α) = -sinα
   • tan(π/2 + α) = -cotα

3. 角与π/2的偶数倍关系：

   • sin(π/2 - α) = cosα
   • cos(π/2 - α) = sinα
   • tan(π/2 - α) = cotα

记忆口诀：奇变偶不变，符号看象限。

同角关系公式

同角关系公式描述了同一角的正弦、余弦、正切等三角函数之间的关系。

1. 平方关系：

   • sin²α + cos²α = 1
   • 1 + tan²α = sec²α
   • 1 + cot²α = csc²α

2. 倒数关系：

   • sinα · cscα = 1
   • cosα · secα = 1
   • tanα · cotα = 1

3. 商数关系：

   • tanα = sinα / cosα
   • cotα = cosα / sinα

和差角公式

和差角公式用于计算两个角的和或差的三角函数值。

1. 正弦和差公式：

   • sin(α + β) = sinα cosβ + cosα sinβ
   • sin(α - β) = sinα cosβ - cosα sinβ

2. 余弦和差公式：

   • cos(α + β) = cosα cosβ - sinα sinβ
   • cos(α - β) = cosα cosβ + sinα sinβ

3. 正切和差公式：

   • tan(α + β) = (tanα + tanβ) / (1 - tanα tanβ)
   • tan(α - β) = (tanα - tanβ) / (1 + tanα tanβ)

倍角公式

倍角公式是和差角公式的特例,用于计算两倍角的三角函数值。

1. 正弦倍角公式：

   sin(2α) = 2 sinα cosα

2. 余弦倍角公式：

   cos(2α) = cos²α - sin²α = 2cos²α - 1 = 1 - 2sin²α

3. 正切倍角公式：

   tan(2α) = 2 tanα / (1 - tan²α)

半角公式

半角公式用于计算一半角的三角函数值。

1. 正弦半角公式：

   sin(α/2) = ±√((1 - cosα) / 2)

2. 余弦半角公式：

   cos(α/2) = ±√((1 + cosα) / 2)

3. 正切半角公式：

   tan(α/2) = ±√((1 - cosα) / (1 + cosα))

和差化积公式

和差化积公式将三角函数的和或差转化为积的形式,常用于简化计算。

1. 正弦和化积：

   • sinα + sinβ = 2 sin((α+β)/2) cos((α-β)/2)
   • sinα - sinβ = 2 cos((α+β)/2) sin((α-β)/2)

2. 余弦和化积：

   • cosα + cosβ = 2 cos((α+β)/2) cos((α-β)/2)
   • cosα - cosβ = -2 sin((α+β)/2) sin((α-β)/2)

记忆技巧与注意事项

1. 记忆技巧：

   • 诱导公式：奇变偶不变，符号看象限。
   • 和差角公式：正弦加正弦，正弦乘余弦加余弦乘正弦。
   • 倍角公式：正弦二倍是二正弦余弦，余弦二倍是余弦平方减正弦平方。

2. 注意事项：

   • 使用公式时注意角的范围,避免符号错误。
   • 在化简过程中，合理选择公式,避免不必要的复杂化。
   • 多练习典型例题,加深对公式的理解。