三角函数公式大全表格30 45 60 90 120:三角函数公式大全,30°45°60°90°120°角度公式表格与实用总结
三角函数是数学中重要的基础内容,尤其在几何、物理和工程学中应用广泛,掌握特殊角度(如30°、45°、60°、90°、120°)的三角函数值及其相关公式,是学习三角函数的关键,本文将通过表格形式整理这些角度的常用公式,并结合恒等式、和差角公式、倍角公式等内容,帮助读者快速掌握三角函数的核心知识。
特殊角度的三角函数值(表格形式)
以下是30°、45°、60°、90°、120°五个特殊角度的六个基本三角函数值(sin、cos、tan、cot、sec、csc):
| 角度(度) | 角度(弧度) | sin θ | cos θ | tan θ | cot θ | sec θ | csc θ |
|---|---|---|---|---|---|---|---|
| 30° | π/6 | 1/2 | √3/2 | √3/3 | √3 | 2/√3 | 2 |
| 45° | π/4 | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| 60° | π/3 | √3/2 | 1/2 | √3 | √3/3 | 2 | 2/√3 |
| 90° | π/2 | 1 | 0 | 无穷大 | 0 | 无穷大 | 1 |
| 120° | 2π/3 | √3/2 | -1/2 | -√3 | -√3/3 | -2 | 2/√3 |
注:
- 90°和120°的tan、sec、csc值在某些情况下可能不适用,因为分母为0或不存在。
- 120°位于第二象限,sin为正,cos为负。
常用三角函数恒等式
毕达哥拉斯恒等式:
- (\sin^2 θ + \cos^2 θ = 1)
- (1 + \tan^2 θ = \sec^2 θ)
- (1 + \cot^2 θ = \csc^2 θ)
互余关系:
- (\sin θ = \cos(90° - θ))
- (\cos θ = \sin(90° - θ))
- (\tan θ = \cot(90° - θ))
和差角公式
正弦和角公式:
- (\sin(A + B) = \sin A \cos B + \cos A \sin B)
- (\sin(A - B) = \sin A \cos B - \cos A \sin B)
余弦和角公式:
- (\cos(A + B) = \cos A \cos B - \sin A \sin B)
- (\cos(A - B) = \cos A \cos B + \sin A \sin B)
正切和角公式:
- (\tan(A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B})
- (\tan(A - B) = \frac{\tan A - \tan B}{1 + \tan A \tan B})
倍角公式
正弦倍角公式:
(\sin 2θ = 2 \sin θ \cos θ)
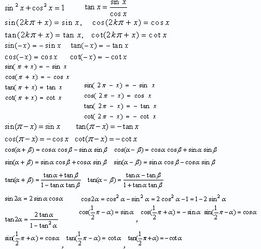
余弦倍角公式:
(\cos 2θ = \cos^2 θ - \sin^2 θ = 2\cos^2 θ - 1 = 1 - 2\sin^2 θ)
正切倍角公式:
(\tan 2θ = \frac{2 \tan θ}{1 - \tan^2 θ})
半角公式
正弦半角公式:
(\sin \frac{θ}{2} = \pm \sqrt{\frac{1 - \cos θ}{2}})
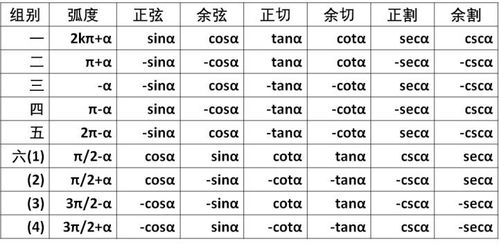
余弦半角公式:
(\cos \frac{θ}{2} = \pm \sqrt{\frac{1 + \cos θ}{2}})
正切半角公式:
(\tan \frac{θ}{2} = \pm \sqrt{\frac{1 - \cos θ}{1 + \cos θ}})
实用技巧与记忆方法
特殊角度的记忆:
- 30°、45°、60° 是三角函数中最常用的特殊角度,建议通过单位圆或几何图形(如等边三角形、直角三角形)来记忆。
- 30-60-90三角形:边长比例为 (1 : \sqrt{3} : 2)。
- 45-45-90三角形:边长比例为 (1 : 1 : \sqrt{2})。
符号记忆:
- 在第二象限(90°~180°),sin为正,cos为负。
- 在第三象限(180°~270°),sin和cos均为负。
- 在第四象限(270°~360°),sin为负,cos为正。
文章已关闭评论!