反三角函数完整图像：反三角函数图像全解析，从定义到图像绘制

反三角函数是三角函数的逆运算，用于求解三角函数中角度与函数值之间的关系，与三角函数不同，反三角函数的定义域和值域受到严格限制，以确保其函数关系的“单值性”，本文将系统介绍六种常见的反三角函数及其完整图像，帮助读者从定义、性质到图像绘制全面理解。

反三角函数的定义与背景

反三角函数是三角函数的逆运算，若 (\sin \theta = x)，则 (\theta = \arcsin x)，由于三角函数（如正弦、余弦、正切）在某些区间内不是一一映射的，因此反三角函数的定义域和值域被限制在一个单调区间内,以确保其函数关系的唯一性。

常见的反三角函数包括：

1. (\arcsin x)（反正弦函数）
2. (\arccos x)（反余弦函数）
3. (\arctan x)（反正切函数）
4. (\operatorname{arccot} x)（反余切函数）
5. (\operatorname{arcsec} x)（反正割函数）
6. (\operatorname{arccsc} x)（反余割函数）

反三角函数图像的绘制与特点

(\arcsin x)（反正弦函数）

• 定义域：([-1, 1])
• 值域：([-\frac{\pi}{2}, \frac{\pi}{2}])
• 图像特点：单调递增，关于原点对称（奇函数），图像在 ([-1, 1]) 上从 ((-\frac{\pi}{2}, -1)) 到 ((\frac{\pi}{2}, 1)) 呈“S”形曲线。

(\arccos x)（反余弦函数）

• 定义域：([-1, 1])
• 值域：([0, \pi])
• 图像特点：单调递减，y 轴对称（偶函数），图像在 ([-1, 1]) 上从 ((-\frac{\pi}{2}, -1)) 到 ((\frac{\pi}{2}, 1)) 呈“拱形”。

(\arctan x)（反正切函数）

• 定义域：((-\infty, +\infty))
• 值域：((-\frac{\pi}{2}, \frac{\pi}{2}))
• 图像特点：单调递增，渐近线为 (y = \frac{\pi}{2}) 和 (y = -\frac{\pi}{2})，图像在 x 轴两侧趋近于渐近线。

(\operatorname{arccot} x)（反余切函数）

• 定义域：((-\infty, +\infty))
• 值域：((0, \pi))
• 图像特点：单调递减，渐近线为 (y = 0) 和 (y = \pi)，图像在 x 轴上方，从 ((-\infty, \pi)) 到 ((+\infty, 0))。

(\operatorname{arcsec} x)（反正割函数）

• 定义域：((-\infty, -1] \cup [1, +\infty))
• 值域：((0, \frac{\pi}{2}) \cup (\frac{\pi}{2}, \pi))
• 图像特点：单调递减，图像在 (x \geq 1) 和 (x \leq -1) 两部分,分别位于第一象限和第二象限。

(\operatorname{arccsc} x)（反余割函数）

• 定义域：((-\infty, -1] \cup [1, +\infty))
• 值域：([-\frac{\pi}{2}, 0) \cup (\frac{\pi}{2}, \pi])
• 图像特点：单调递减，图像在 (x \geq 1) 和 (x \leq -1) 两部分,分别位于第一象限和第二象限。

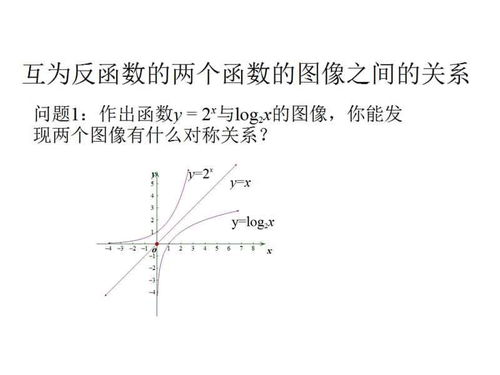
反三角函数图像的对称性与关系

反三角函数之间存在一定的对称关系，

• (\arcsin x + \arccos x = \frac{\pi}{2})
• (\arctan x + \operatorname{arccot} x = \frac{\pi}{2})

这些关系可以通过图像直观地理解，(\arcsin x) 和 (\arccos x) 的图像关于直线 (y = \frac{\pi}{2} - x) 对称。

反三角函数的图像具有鲜明的特征，其定义域和值域的限制确保了函数的“单值性”，通过绘制这些图像，我们可以直观地理解反三角函数的性质，如单调性、渐近线、对称性等，掌握这些图像,对于解决涉及角度与函数值的数学问题具有重要意义。

希望本文能帮助读者更好地理解反三角函数的图像与性质,为后续的数学学习打下坚实基础。