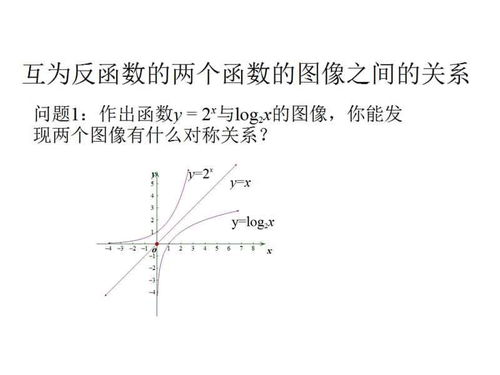
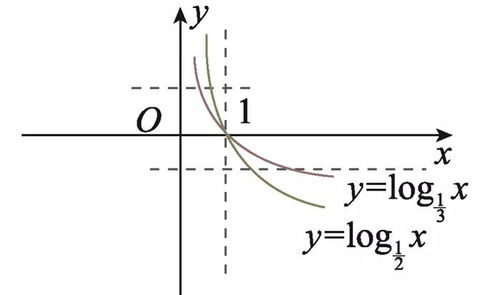初二函数怎么学最简单方法：轻松搞定初二函数，最简单易懂的学习方法！

函数,是初中数学的一个重要章节，也是很多同学觉得有点抽象、有点难入门的知识点，别担心！掌握几个简单实用的方法，函数学习也能变得轻松有趣，今天就来分享几个最简单、最有效的学习函数的方法。

核心理念：从生活实例出发，理解“输入”与“输出”的关系

函数的本质,就是研究一个量变化时，另一个量如何随之变化的关系，它描述的是“输入”和“输出”之间的规则。

最简单学习方法详解：

第一步：吃透基本概念，抓住核心（理解是基础）

1. 认识函数： 想象一下，你有一个“魔法盒子”，你往里面放一个数（输入，自变量），盒子根据一个固定的规则（函数本身），会吐出另一个数（输出，因变量），一个简单的函数 y = 2x，你输入 x=3，输出 y=6；输入 x=5，输出 y=10，关键在于，同一个输入 x，必须得到唯一的输出 y。
2. 理解自变量和因变量： 自变量 x 是你主动选择或改变的量（输入），因变量 y 是依赖于 x 而变化的量（输出），它们之间的关系就是函数关系 y = f(x)。
3. 认识函数的表示法：
   • 关系式： 就是我们最常见的 y = 2x + 1 这种形式，这是最直接、最常用的方式。
   • 表格法： 列表， | x (输入) | 1 | 2 | 3 | | :------- | :- | :- | :- | | y (输出) | 3 | 5 | 7 | 这个表格表示了一个函数关系 y = 2x + 1。
   • 图像法： 在坐标系中画图，横轴通常是自变量 x，纵轴是因变量 y，点 (x, y) 在图像上，意味着当输入 x 时，输出是 y，图像法能直观地展示函数的变化趋势。这是理解函数最直观、最重要的方法之一！

第二步：多做练习，熟能生巧（实践是关键）

1. 模仿例题： 认真看课本或老师讲解的例题，理解解题步骤和思路，尝试模仿着做类似的题目。
2. 动手画图： 这是最简单也最有效的学习方法之一！
   • 坐标系是你的朋友： 熟悉坐标系，知道横轴是 x，纵轴是 y。
   • 描点画图： 对于给定的关系式，y = x + 1，你可以选择几个 x 值（-1, 0, 1, 2），计算出对应的 y 值（0, 1, 2, 3），然后在坐标系中找到点 (-1, 0), (0, 1), (1, 2), (2, 3)，把它们连起来（如果是直线就是一条直线，如果是曲线就是一条曲线）。看着图像，你能立刻想象出“输入” x 和“输出” y 的关系是怎样的。
   • 观察图像： 通过图像，你可以直观地看出函数是递增还是递减，最大值、最小值在哪里，以及整体的变化趋势。

第三步：联系生活，学以致用（理解才有动力）

• 寻找生活中的函数： 函数其实无处不在！
  • 圆的周长 C = 2πr，半径 r 是自变量，周长 C 是因变量。
  • 火车行驶的距离 s = v * t，时间 t 是自变量，距离 s 是因变量。
  • 水池注水,水的高度 h 随着注水时间 t 或注水量 V 的增加而增加。
  • 尝试用函数关系式或图像来描述这些现象,这能让你深刻体会到学习函数的意义，不再觉得它是枯燥的符号。

第四步：总结规律，查漏补缺（巩固是保障）

• 归纳常见函数类型： 初二是学习一次函数（y = kx + b）、正比例函数（y = kx）等，理解它们图像（直线）的特点，以及 k 和 b 的影响（斜率和截距）。
• 整理错题： 做错的题目是最好的复习资料，分析错误原因，是概念不清？还是计算失误？是画图不准？下次遇到类似题目就能避免。
• 多问多想： 遇到不懂的地方，及时问老师或同学，思考“为什么”是这样定义的？这个规则能怎么用？

简单学习函数的要点总结：

• 核心是理解“输入-输出”关系。
• 图像法是理解函数最直观的方法，一定要多画图！
• 联系生活实际，让数学变得有意义。
• 多做练习，熟能生巧。
• 抓住基本概念，尤其是自变量、因变量、函数表示法。

最后提醒：

学习任何知识都需要时间和耐心,找到适合自己的方法，坚持下去，你会发现函数并没有想象中那么难，加油！