对数函数的反函数：对数函数的反函数，定义、图像与应用

反函数的定义

设函数 ( f ) 的定义域为 ( D )，值域为 ( R )，如果存在一个函数 ( g )，使得对于所有 ( x \in D )，有 ( g(f(x)) = x )，且对于所有 ( y \in R )，有 ( f(g(y)) = y )，则称 ( g ) 是 ( f ) 的反函数，记作 ( g = f^{-1} )。

反函数的定义要求原函数必须是一一映射（即单射且满射）,这样才能保证反函数存在且唯一。

对数函数及其反函数

对数函数的定义

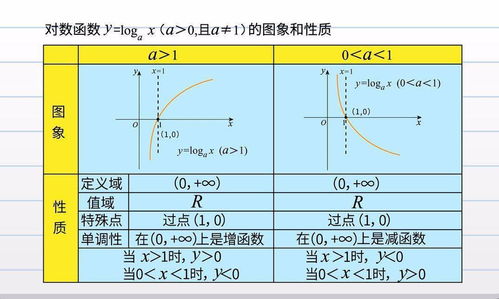
对数函数 ( y = \log_b x )（( b > 0 ) 且 ( b \neq 1 )）定义在 ( x > 0 ) 的区间上，其底数 ( b ) 决定了函数的单调性，当 ( b > 1 ) 时，函数单调递增；当 ( 0 < b < 1 ) 时,函数单调递减。

对数函数的反函数

对数函数的反函数是指数函数，即 ( y = b^x )，根据反函数的定义，若 ( y = \log_b x )，则 ( x = b^y )，因此指数函数 ( y = b^x ) 就是对数函数 ( y = \log_b x ) 的反函数。

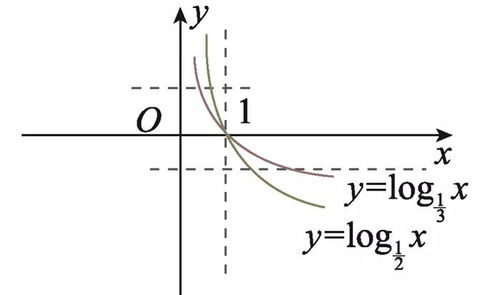
以自然对数函数 ( y = \ln x )（底数为 ( e )）为例，其反函数为 ( y = e^x )。

图像与性质

图像关系

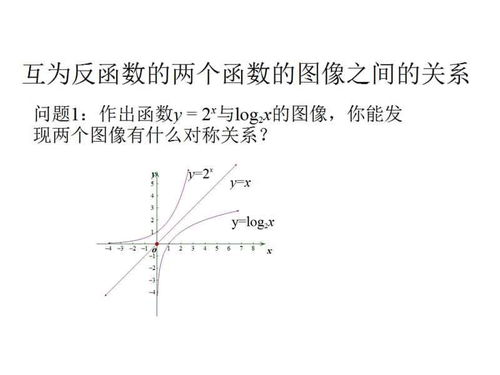
对数函数与指数函数的图像关于直线 ( y = x ) 对称，函数 ( y = \log_2 x ) 与 ( y = 2^x ) 的图像关于 ( y = x ) 对称。

定义域与值域

• 对数函数 ( y = \log_b x ) 的定义域为 ( (0, +\infty) )，值域为 ( \mathbb{R} )。
• 指数函数 ( y = b^x ) 的定义域为 ( \mathbb{R} )，值域为 ( (0, +\infty) )。

单调性

• 当 ( b > 1 ) 时,对数函数和指数函数均单调递增。
• 当 ( 0 < b < 1 ) 时,对数函数和指数函数均单调递减。

特殊点

• 对数函数 ( y = \log_b x ) 经过点 ( (1, 0) )（因为 ( \log_b 1 = 0 )）。
• 指数函数 ( y = b^x ) 经过点 ( (0, 1) )（因为 ( b^0 = 1 )）。

应用实例

解对数方程

利用反函数可以快速求解对数方程，求解方程 ( \log_2 x = 3 )：

由反函数性质，( x = 2^3 = 8 )。

指数增长与衰减模型

在自然科学中，许多现象可以用指数函数描述，如放射性元素的衰变、人口增长等，对数函数则用于反向计算,例如计算半衰期或增长率。

数据压缩与信息论

在信息论中，对数函数及其反函数用于计算信息熵和数据压缩的效率,是现代通信技术的基础。

对数函数的反函数是指数函数，两者通过图像对称和定义域、值域的互换紧密联系，理解反函数的概念不仅有助于掌握对数与指数函数的性质，还能在实际问题中灵活应用，无论是数学学习还是科学计算,对数函数及其反函数都发挥着重要作用。