指数函数积分公式：指数函数积分公式，从推导到应用

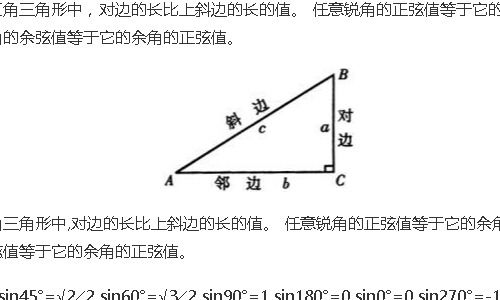
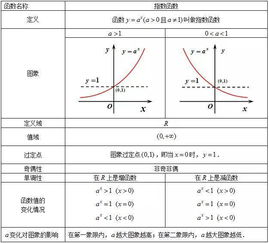
指数函数的定义与性质

指数函数通常定义为 ( f(x) = a^x )，( a > 0 ) 且 ( a \neq 1 )，当 ( a = e )（自然对数的底）时，函数 ( f(x) = e^x ) 称为自然指数函数，其导数和积分形式最为简洁。

指数函数具有以下重要性质：

1. ( a^{x+y} = a^x \cdot a^y )
2. ( a^{xy} = (a^x)^y )
3. ( \frac{d}{dx} a^x = a^x \ln a )

指数函数的积分公式

指数函数的积分公式如下：

[ \int a^x dx = \frac{a^x}{\ln a} + C ]

( a > 0 ) 且 ( a \neq 1 )，( \ln a ) 是 ( a ) 的自然对数，( C ) 是积分常数。

当 ( a = e ) 时，公式简化为：

[ \int e^x dx = e^x + C ]

积分公式的推导

为了推导指数函数的积分公式,我们可以使用换元法，设 ( u = a^x )，则 ( du = a^x \ln a dx )，

[ dx = \frac{du}{u \ln a} ]

代入积分式：

[ \int a^x dx = \int u \cdot \frac{du}{u \ln a} = \frac{1}{\ln a} \int du = \frac{u}{\ln a} + C = \frac{a^x}{\ln a} + C ]

对于 ( e^x ) 的积分，由于 ( \ln e = 1 )，

[ \int e^x dx = e^x + C ]

应用示例

求解 ( \int 2^x dx )

根据公式：

[ \int 2^x dx = \frac{2^x}{\ln 2} + C ]

求解 ( \int e^{2x} dx )

令 ( u = 2x )，则 ( du = 2 dx )，

[ \int e^{2x} dx = \frac{1}{2} \int e^u du = \frac{1}{2} e^u + C = \frac{1}{2} e^{2x} + C ]

实际应用

指数函数的积分在许多领域有重要应用,

1. 放射性衰变：描述放射性物质的衰变过程。
2. 人口增长模型：用于预测人口增长趋势。
3. 电路分析：在RC电路中描述电荷的积累。
4. 金融数学：计算复利和连续增长。