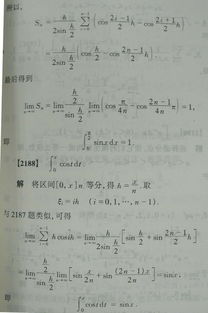三角函数计算方法：三角函数计算方法全解析

基于定义的计算方法

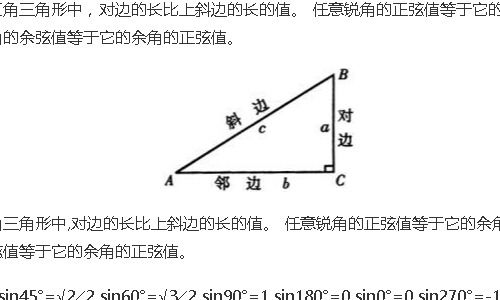
三角函数的定义是计算的基础，以单位圆上的点坐标为基础，可以定义正弦（sin）、余弦（cos）和正切（tan）等基本三角函数。

• 正弦函数：sinθ = 对边 / 斜边
• 余弦函数：cosθ = 邻边 / 斜边
• 正切函数：tanθ = 对边 / 邻边

在一个直角三角形中，若角θ的对边为3，斜边为5，则sinθ = 3/5 = 0.6。

使用计算器或计算机

现代计算工具如科学计算器、数学软件（如MATLAB、Mathematica）或编程语言（如Python、Java）都可以快速计算三角函数值。

在Python中，可以使用math模块计算三角函数：

import math
angle_in_degrees = 30
angle_in_radians = math.radians(angle_in_degrees)
sin_value = math.sin(angle_in_radians)
cos_value = math.cos(angle_in_radians)
tan_value = math.tan(angle_in_radians)
print(f"sin(30°) = {sin_value}")
print(f"cos(30°) = {cos_value}")
print(f"tan(30°) = {tan_value}")

输出结果为：

sin(30°) = 0.5
cos(30°) = 0.8660254037844386
tan(30°) = 0.5773502691896257

使用三角恒等式

三角恒等式是计算复杂三角函数值的有效工具,常用的恒等式包括：

• 毕达哥拉斯恒等式：sin²θ + cos²θ = 1
• 和角公式：sin(α + β) = sinα cosβ + cosα sinβ
• 差角公式：cos(α - β) = cosα cosβ + sinα sinβ

计算sin(15°)：

sin(15°) = sin(45° - 30°) = sin45° cos30° - cos45° sin30°
sin45° = √2/2 ≈ 0.7071, cos30° = √3/2 ≈ 0.8660, cos45° = √2/2 ≈ 0.7071, sin30° = 0.5
sin(15°) = (0.7071 × 0.8660) - (0.7071 × 0.5) ≈ 0.6123 - 0.3536 ≈ 0.2587

使用泰勒级数展开

泰勒级数展开是数值计算三角函数的一种方法,尤其适用于小角度或高精度计算。

sin(x)的泰勒级数展开为：

sin(x) = x - x³/3! + x⁵/5! - x⁷/7! + ...

其中x为弧度制的角度。

计算sin(0.1)：

sin(0.1) ≈ 0.1 - (0.1)³/6 + (0.1)⁵/120 ≈ 0.1 - 0.0001667 + 0.000000833 ≈ 0.099834

使用图形法

在几何中，可以通过绘制单位圆或三角形来直观计算三角函数值，通过单位圆上的点坐标可以确定sinθ和cosθ的值。

数值方法

在计算机科学中，三角函数的计算通常使用数值方法，如CORDIC算法（Coordinate Rotation Digital Computer），它是一种迭代算法，适用于硬件实现,如FPGA或GPU中的三角函数计算。

三角函数的计算方法多种多样，从基本的定义法到高级的数值方法，读者可以根据具体需求选择合适的方法，掌握这些方法不仅可以提高数学解题能力，还能为后续学习高等数学、物理和工程打下坚实基础。

无论是通过计算器、恒等式还是级数展开,灵活运用这些工具都能帮助我们更高效地解决实际问题。