正弦三角函数值表:正弦三角函数值表,从基础到应用
正弦函数的定义与意义
正弦函数是周期函数,其周期为 (2\pi),在数学中具有广泛的应用,在几何中,正弦函数可以用来计算三角形的边长和角度;在物理学中,正弦函数常用于描述简谐振动、波的传播等现象。
正弦三角函数值表的常见角度
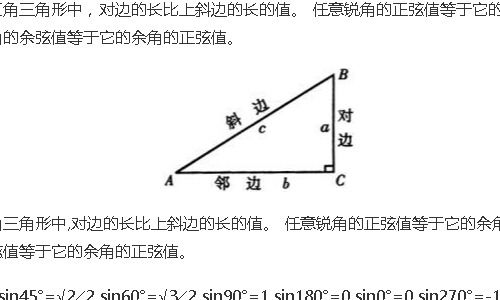
以下是几个特殊角度的正弦函数值,这些角度在学习和应用中非常常见:
| 角度(度) | 角度(弧度) | 正弦值(sin) |
|---|---|---|
| 0° | 0 | 0 |
| 30° | (\frac{\pi}{6}) | (\frac{1}{2}) |
| 45° | (\frac{\pi}{4}) | (\frac{\sqrt{2}}{2}) |
| 60° | (\frac{\pi}{3}) | (\frac{\sqrt{3}}{2}) |
| 90° | (\frac{\pi}{2}) | 1 |
| 180° | (\pi) | 0 |
| 270° | (\frac{3\pi}{2}) | -1 |
| 360° | (2\pi) | 0 |
这些值可以通过几何构造或单位圆来推导,是学习三角函数的基础。
正弦值表的使用方法
正弦值表在实际计算中非常有用,尤其是在没有计算器的情况下。
- 在几何问题中,可以通过正弦值表求解三角形的边长或角度。
- 在工程计算中,正弦函数用于计算力、电压、电流等的周期性变化。
- 在导航和地理学中,正弦函数用于计算距离和方向。
使用正弦值表时,只需找到对应的角度,即可得到其正弦值,对于非特殊角度,通常使用近似值或通过计算器获得。
如何记忆正弦值表?
对于特殊角度的正弦值,可以通过以下方法记忆:
- 单位圆法:想象单位圆上的点,正弦值对应纵坐标。
- 口诀法:对于0°、30°、45°、60°、90°,可以记忆为“0,二分之一,二分之根号二,二分之根号三,1”。
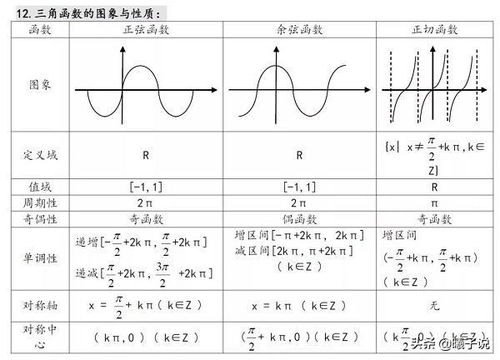
正弦函数的图像与性质
正弦函数的图像是一条波浪线,具有以下性质:
- 周期性:每 (2\pi) 重复一次。
- 对称性:关于原点对称(奇函数)。
- 取值范围:([-1, 1])。
正弦三角函数值表是学习和应用三角函数的基础工具,掌握常见角度的正弦值,不仅有助于解决数学问题,还能为后续学习微积分、物理等学科打下坚实的基础,在实际应用中,可以通过值表、计算器或数学软件快速获取所需数据,提高计算效率。
如果你需要更详细的正弦值表或特定角度的计算,可以使用科学计算器或在线数学工具进行查询。
相关文章:
文章已关闭评论!