c语言求最大公约数与最小公倍数：C语言求最大公约数与最小公倍数，两种经典算法解析

最大公约数（GCD）的求解方法

穷举法

思路：从两个数中较小的数开始，逐个递减尝试,找到能同时整除两个数的最大整数。

步骤：

1. 确定两个数中较小的数；
2. 从该数开始递减,检查是否能同时整除两个数；
3. 找到第一个满足条件的数即为最大公约数。

代码示例：

#include <stdio.h>
int gcd(int a, int b) {
    int min = (a > b) ? b : a; // 获取较小值
    for (int i = min; i >= 1; i--) {
        if (a % i == 0 && b % i == 0) {
            return i; // 返回最大公约数
        }
    }
    return 1; // 默认返回1，理论上两个数至少有一个公约数1
}
int main() {
    int num1, num2;
    printf("请输入两个正整数：");
    scanf("%d %d", &num1, &num2);
    printf("最大公约数是：%d\n", gcd(num1, num2));
    return 0;
}

优点：逻辑简单，易于理解。
缺点：效率较低，尤其当两个数较大时,计算时间较长。

欧几里得算法（辗转相除法）

思路：利用数学定理：若 ( a \div b ) 的余数为 ( r )，则 ( \text{GCD}(a, b) = \text{GCD}(b, r) )，重复此过程直到余数为0,此时除数即为最大公约数。

步骤：

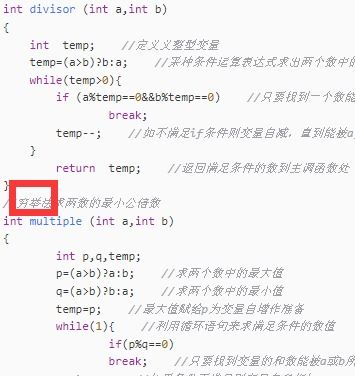
1. 用较大的数除以较小的数,得到余数；
2. 用较小的数除以余数,重复此过程；
3. 当余数为0时,最后一个非零余数即为最大公约数。

代码示例：

#include <stdio.h>
int gcd(int a, int b) {
    while (b != 0) {
        int temp = b;
        b = a % b; // 取余数
        a = temp; // 将b的值赋给a，实现辗转相除
    }
    return a; // 返回最大公约数
}
int main() {
    int num1, num2;
    printf("请输入两个正整数：");
    scanf("%d %d", &num1, &num2);
    printf("最大公约数是：%d\n", gcd(num1, num2));
    return 0;
}

优点：效率高，时间复杂度为 ( O(\log n) )。
缺点：对数学原理有一定要求,初学者可能不易理解。

最小公倍数（LCM）的求解方法

最小公倍数可以通过最大公约数来计算，利用公式：
[ \text{LCM}(a, b) = \frac{|a \times b|}{\text{GCD}(a, b)} ]

步骤：

1. 先求出两个数的最大公约数；
2. 用两个数的乘积除以最大公约数,得到最小公倍数。

代码示例：

#include <stdio.h>
int gcd(int a, int b) {
    while (b != 0) {
        int temp = b;
        b = a % b;
        a = temp;
    }
    return a;
}
int lcm(int a, int b) {
    int result = (a * b) / gcd(a, b); // 利用公式计算最小公倍数
    return result;
}
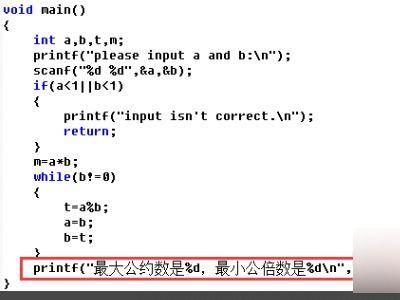
int main() {
    int num1, num2;
    printf("请输入两个正整数：");
    scanf("%d %d", &num1, &num2);
    printf("最小公倍数是：%d\n", lcm(num1, num2));
    return 0;
}

注意：此方法假设输入为正整数，若输入为0或负数,需额外处理。

• 最大公约数：穷举法适合小数计算,欧几里得算法适合大数计算。
• 最小公倍数：可通过最大公约数公式快速求解。
• 实际应用：在分数简化、时间计算、算法设计等领域有广泛应用。

通过本文，读者可以掌握两种经典算法的实现方法，并根据实际需求选择合适的解法，如需进一步优化或处理特殊情况（如负数、零值）,可在此基础上进行扩展。